题目2.1 - 连结主义神经元
该练习用到的数据集Apples Oranges,数据存储两个分类,有200组数据,有两列属性以及一列分类。用简单的神经元对样本进行分类,每个样本
第一题是画散点图,因为只有x.1和x.2两个属性,并且只是一个二分类问题,笔者用R画出散点图(源码):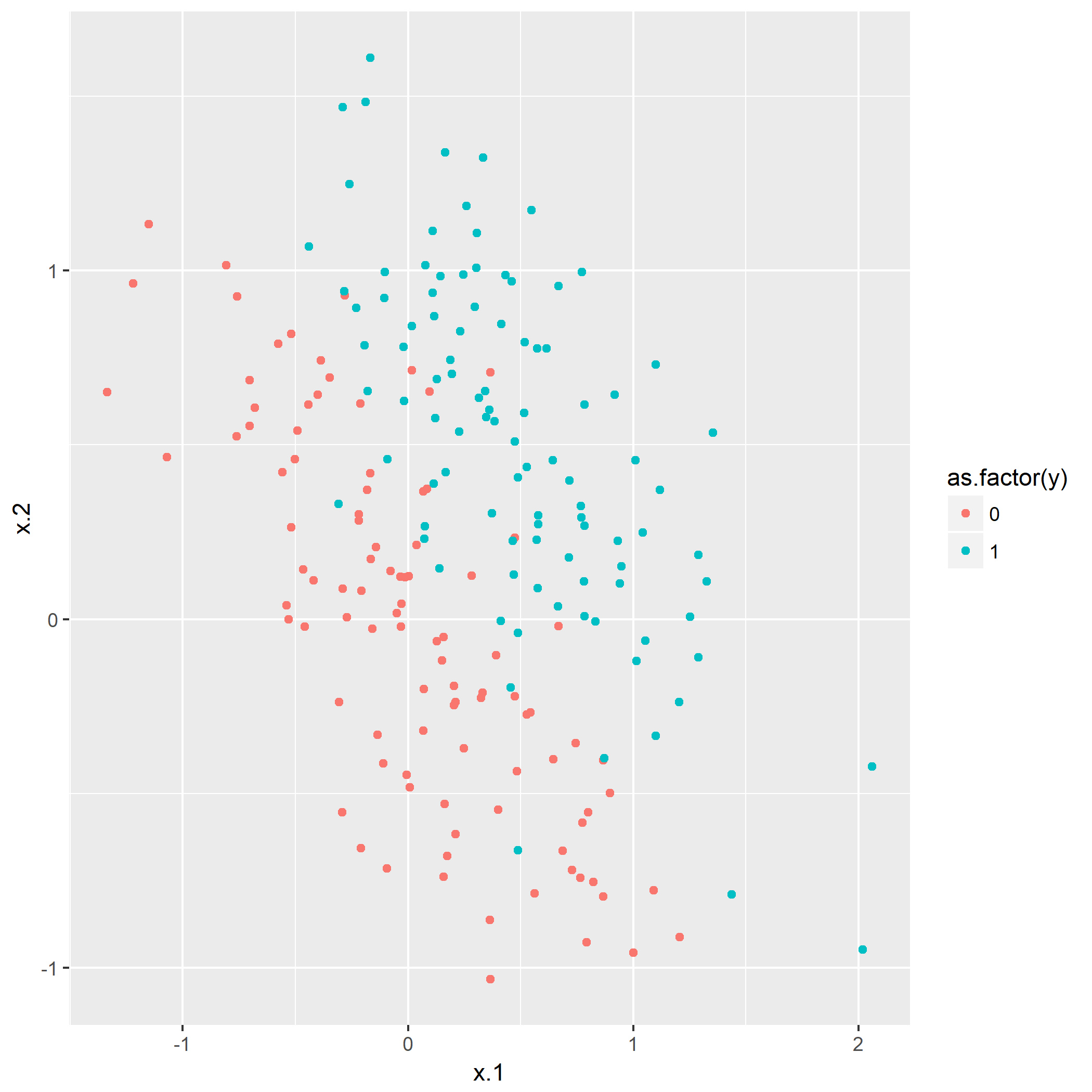
可以看到,还是比较容易分类的。
然后第二题就是设置10°为间隔以及
因为刚好只有两个属性,
将每个正确率-角度的图(源码):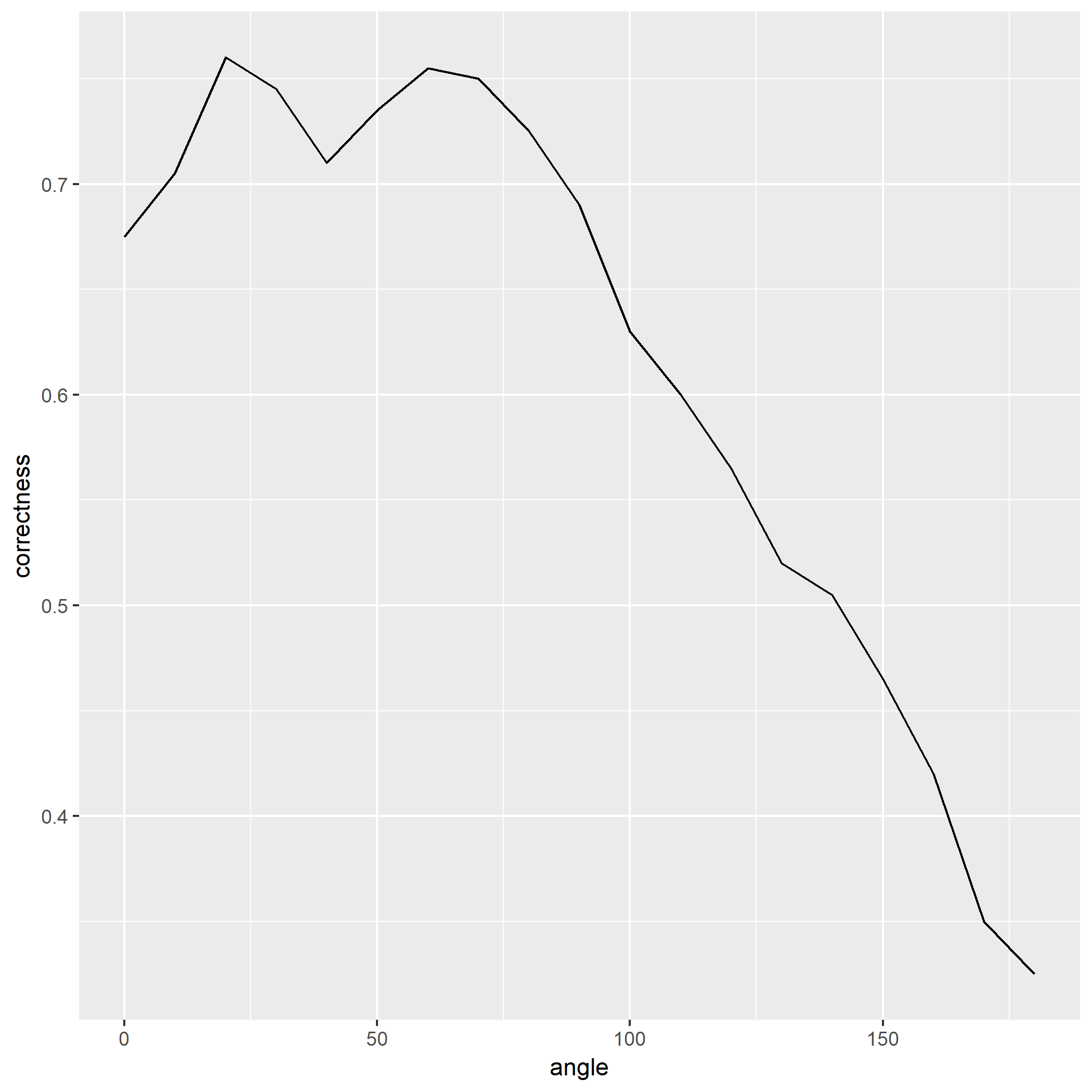
注意
笔者在第二问就尝试输出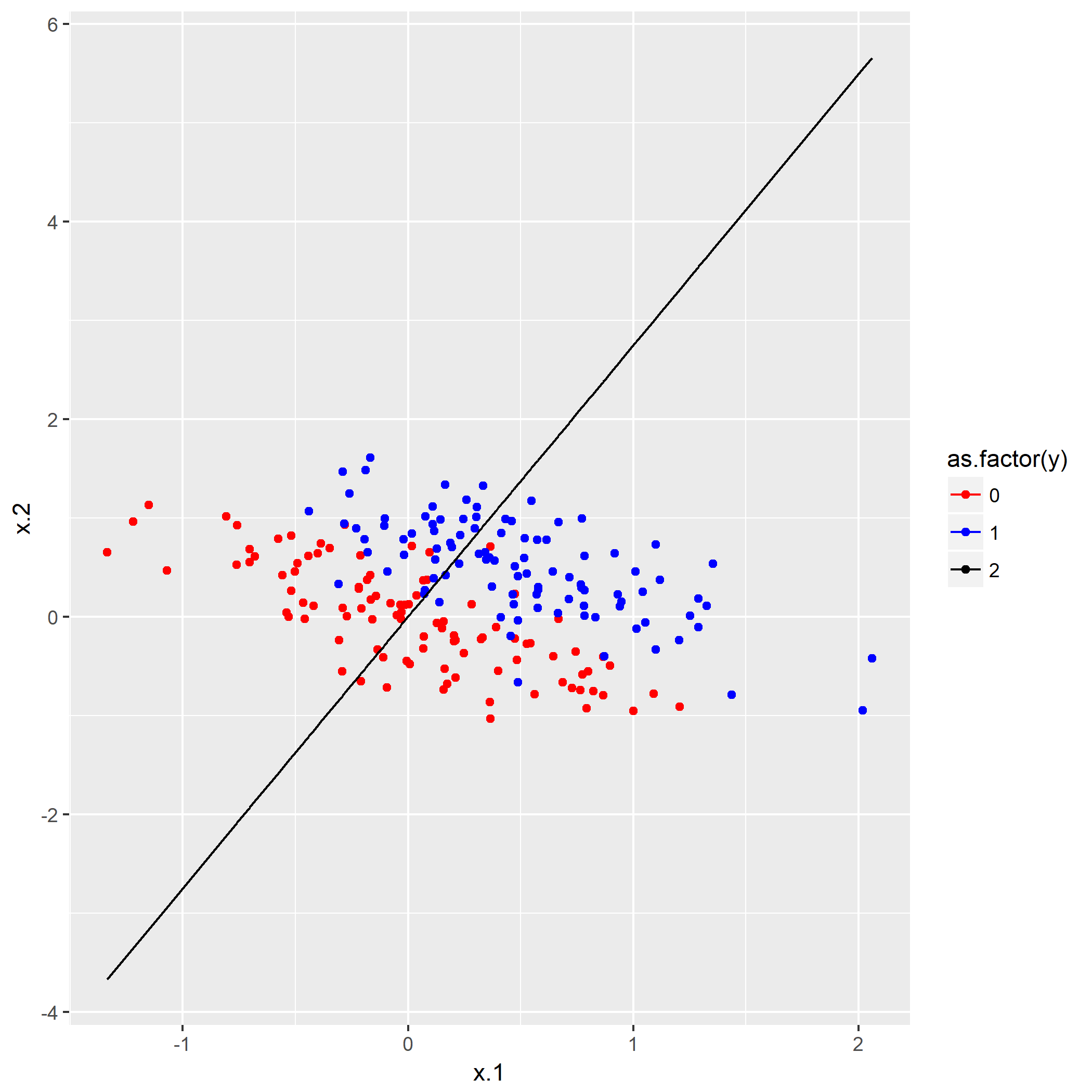
在开始探究原因之前,先回想清楚法向量的定义。
定义是没有问题的,那是因为刚好
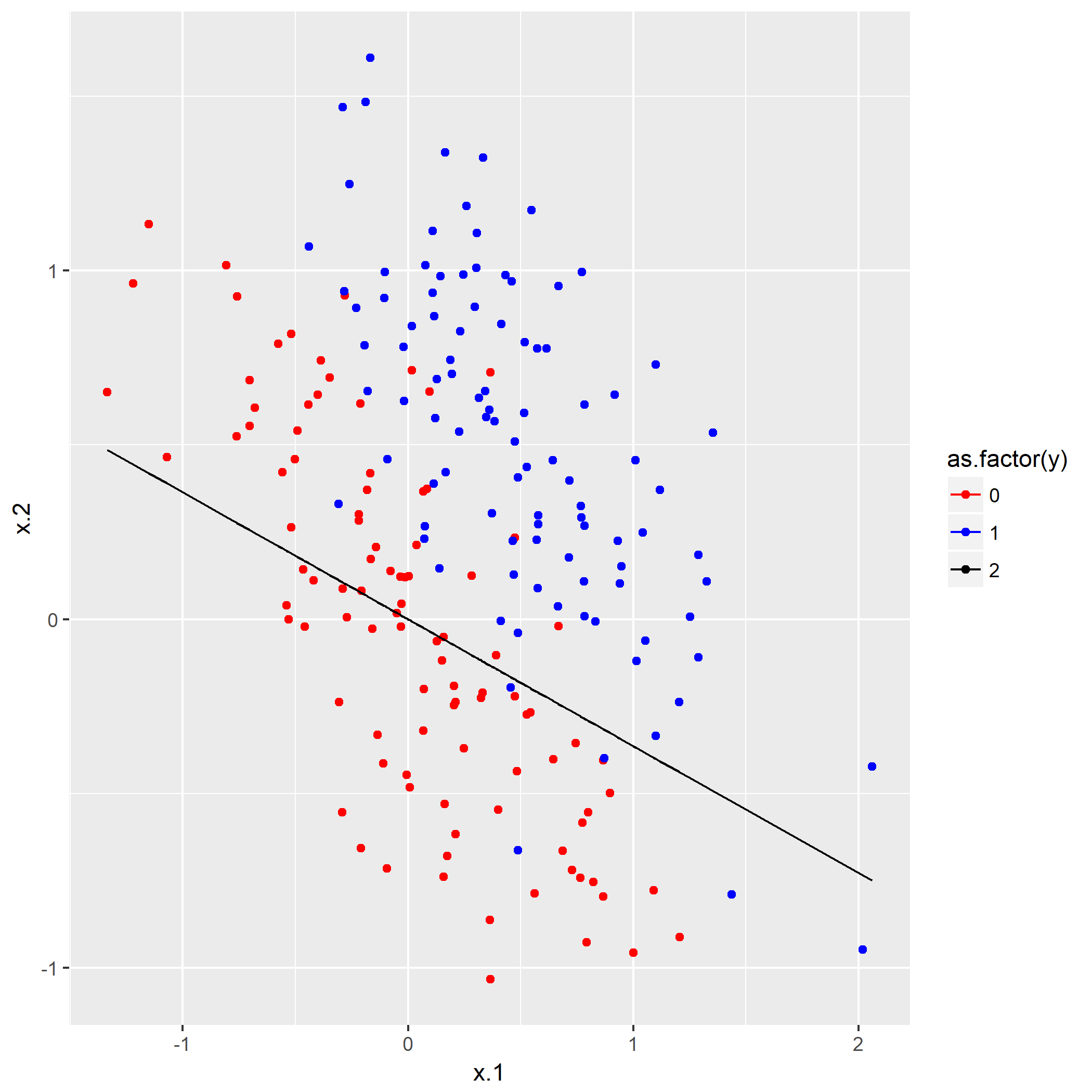
这样才有点像划分的样子,但是要注意这仅仅是
接下来一问是根据上一问得出的最佳的
运行得到:
接下来是根据前两问得出来的
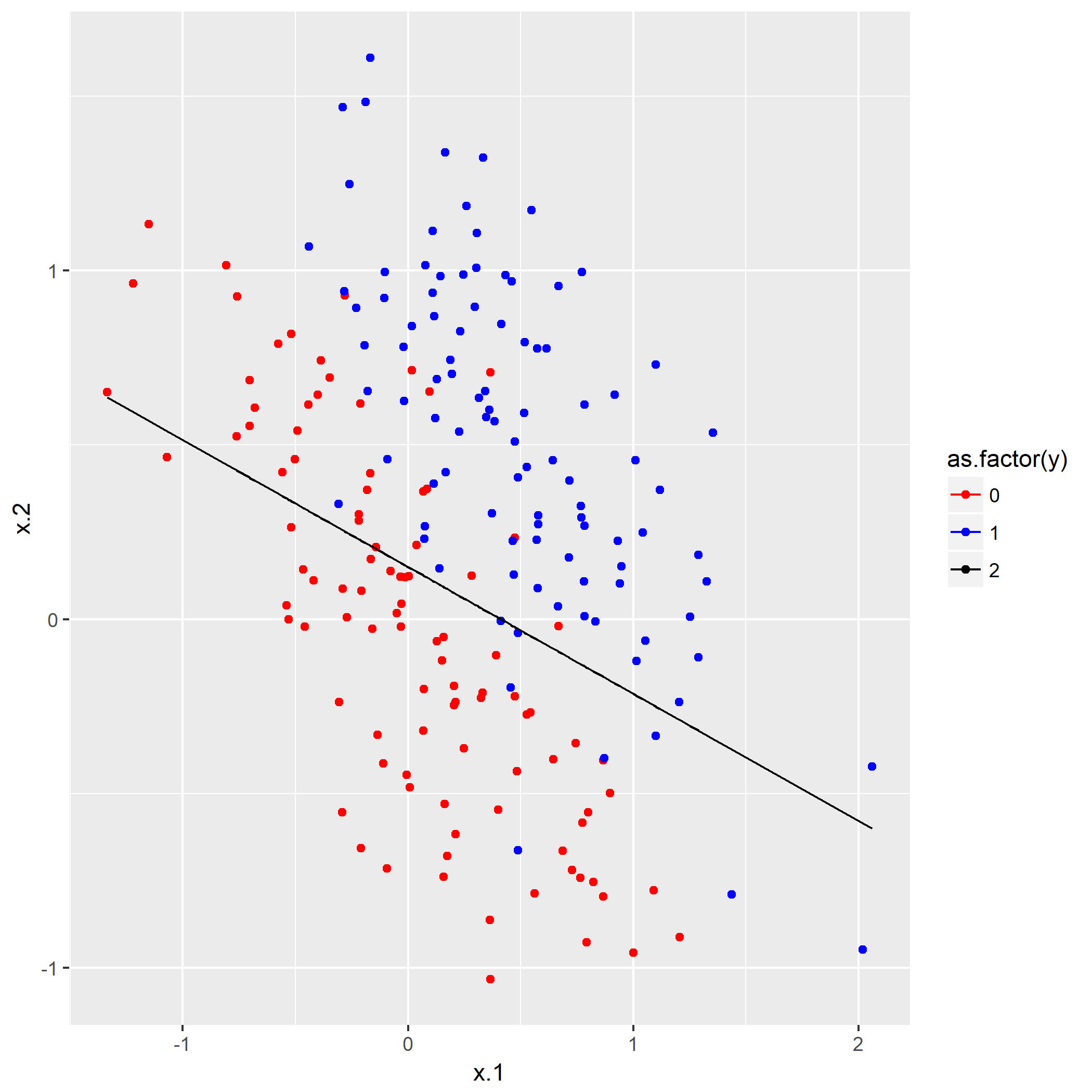
然后就是尝试
运行代码画图:
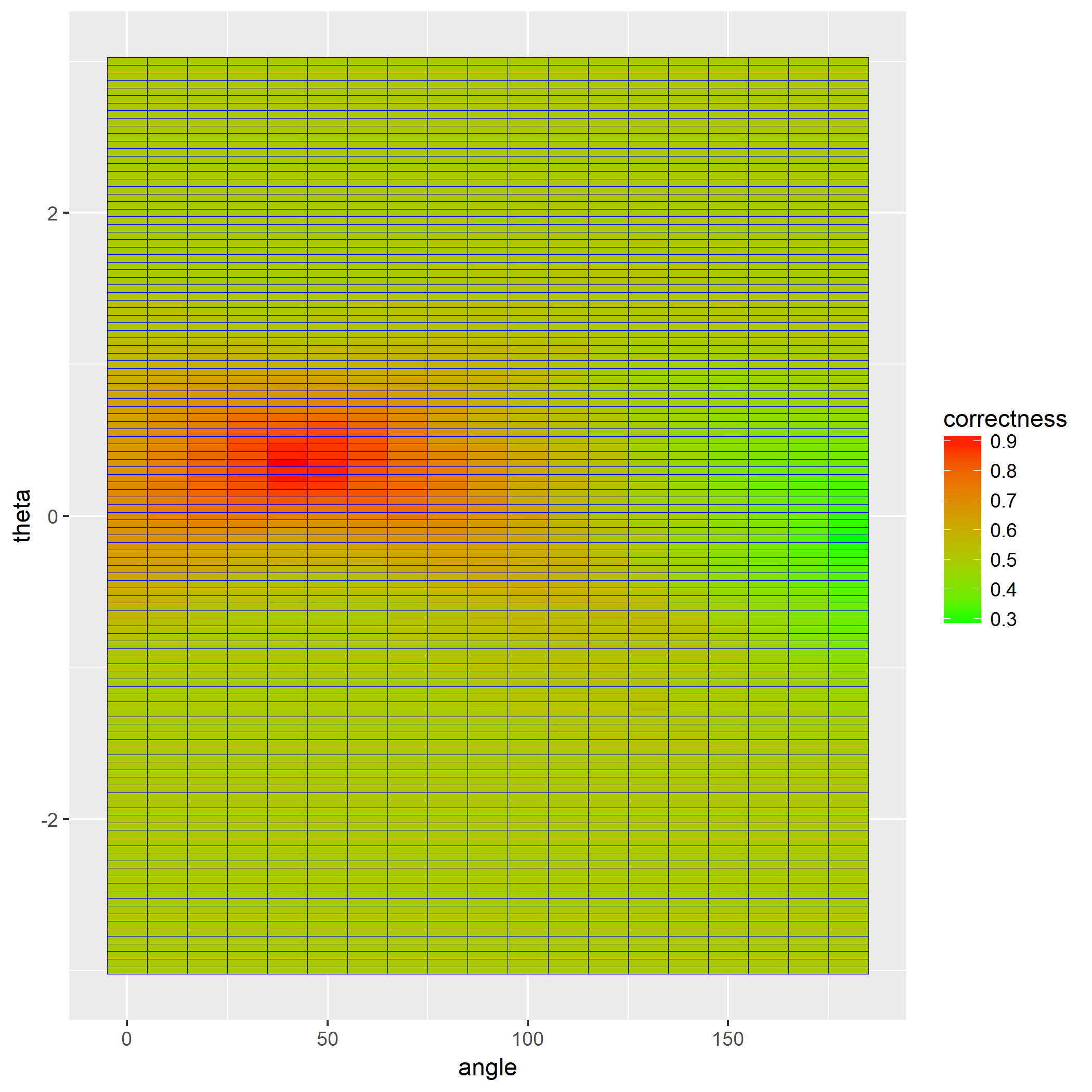
可以肉眼看出正确率较高时的组合在哪个部分。
笔者额外求得最高正确率时的
1 | angle theta w1 w2 correctness |
并作图:
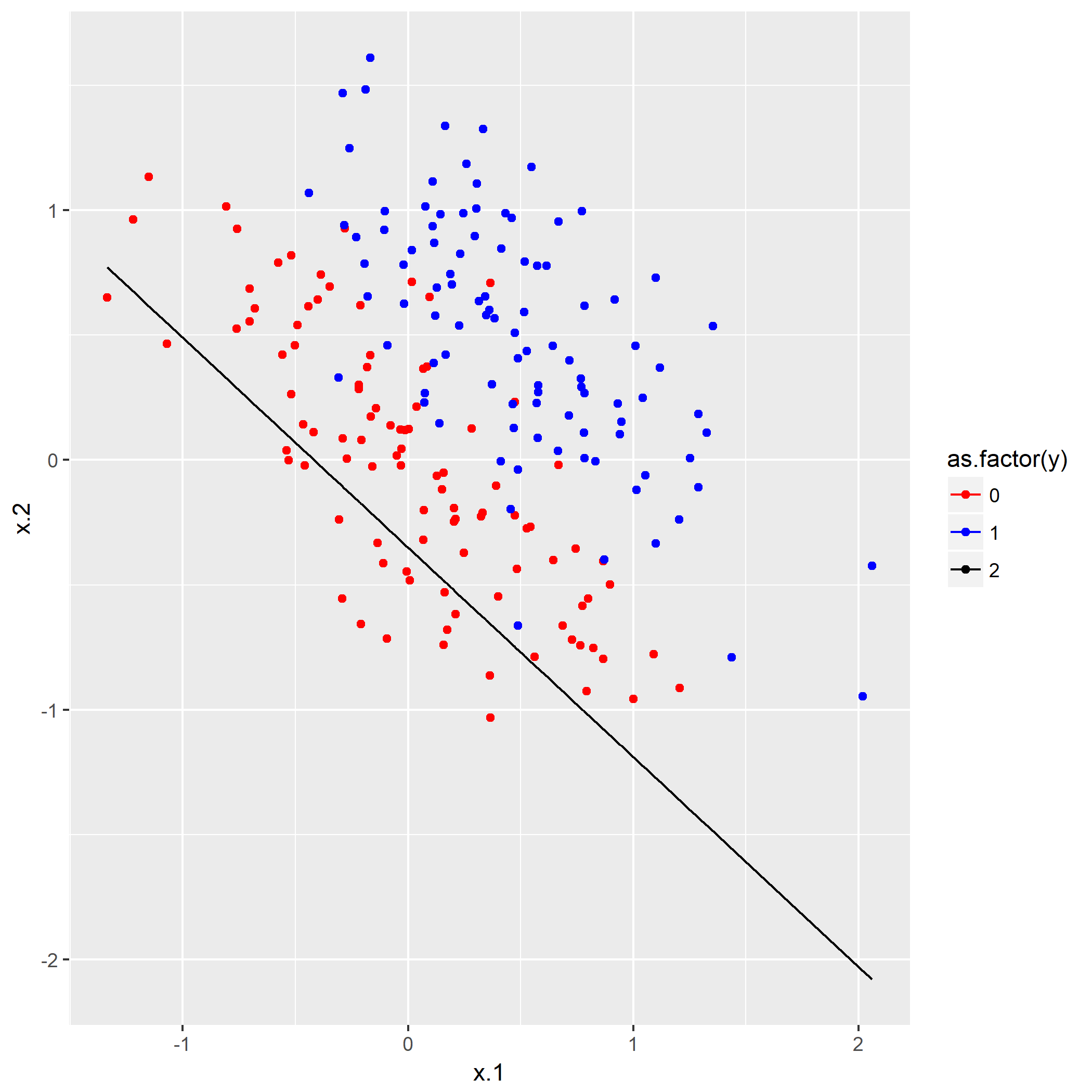
根据方程
原因是在笔者画线是所用的方程
题目2.2 - 多层感知机
该题目是简单地体验一下多层感知机,假设其中一层隐藏层,该层有10个感知机,通过随机生成
第一问设置
对于
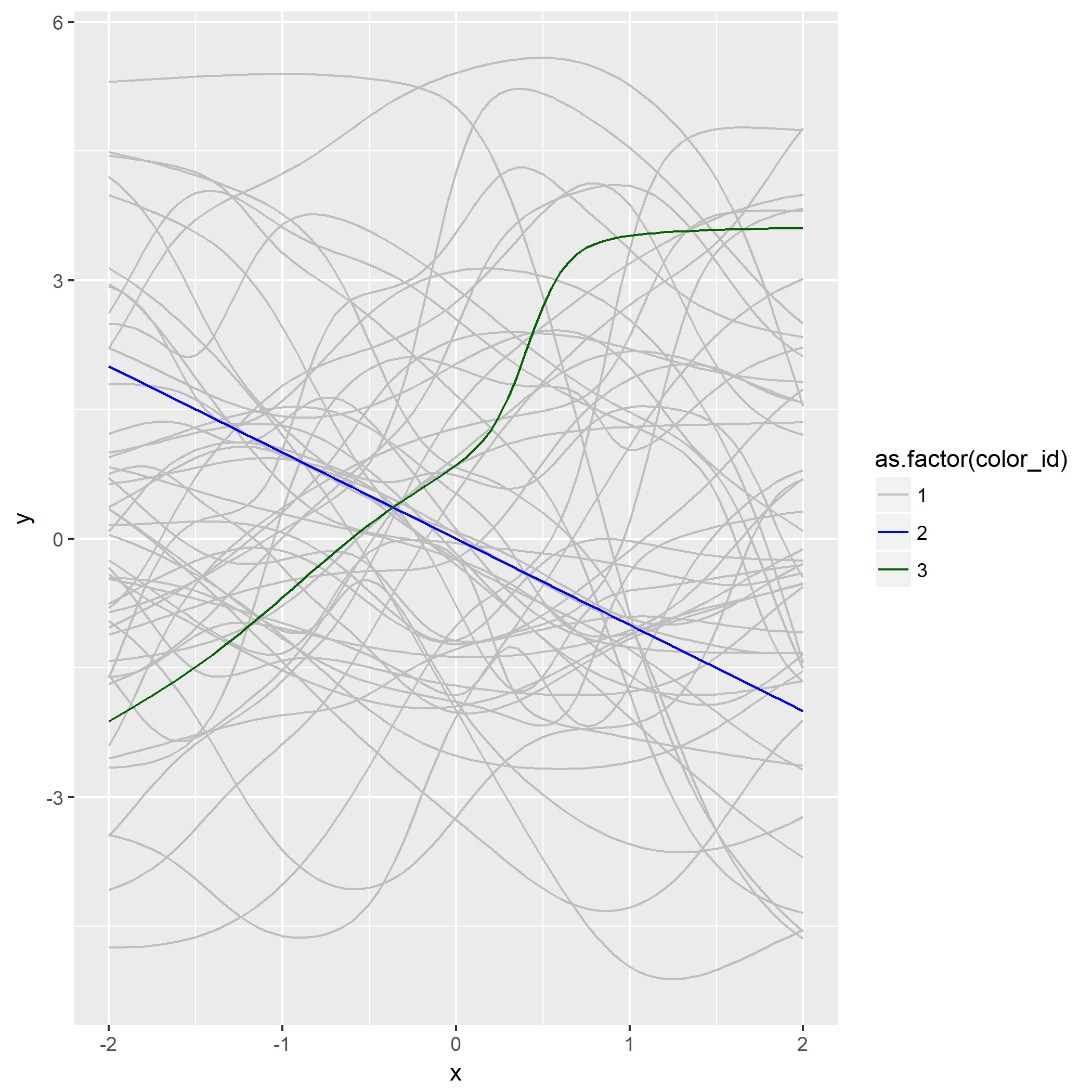
第二问改成:
得到:
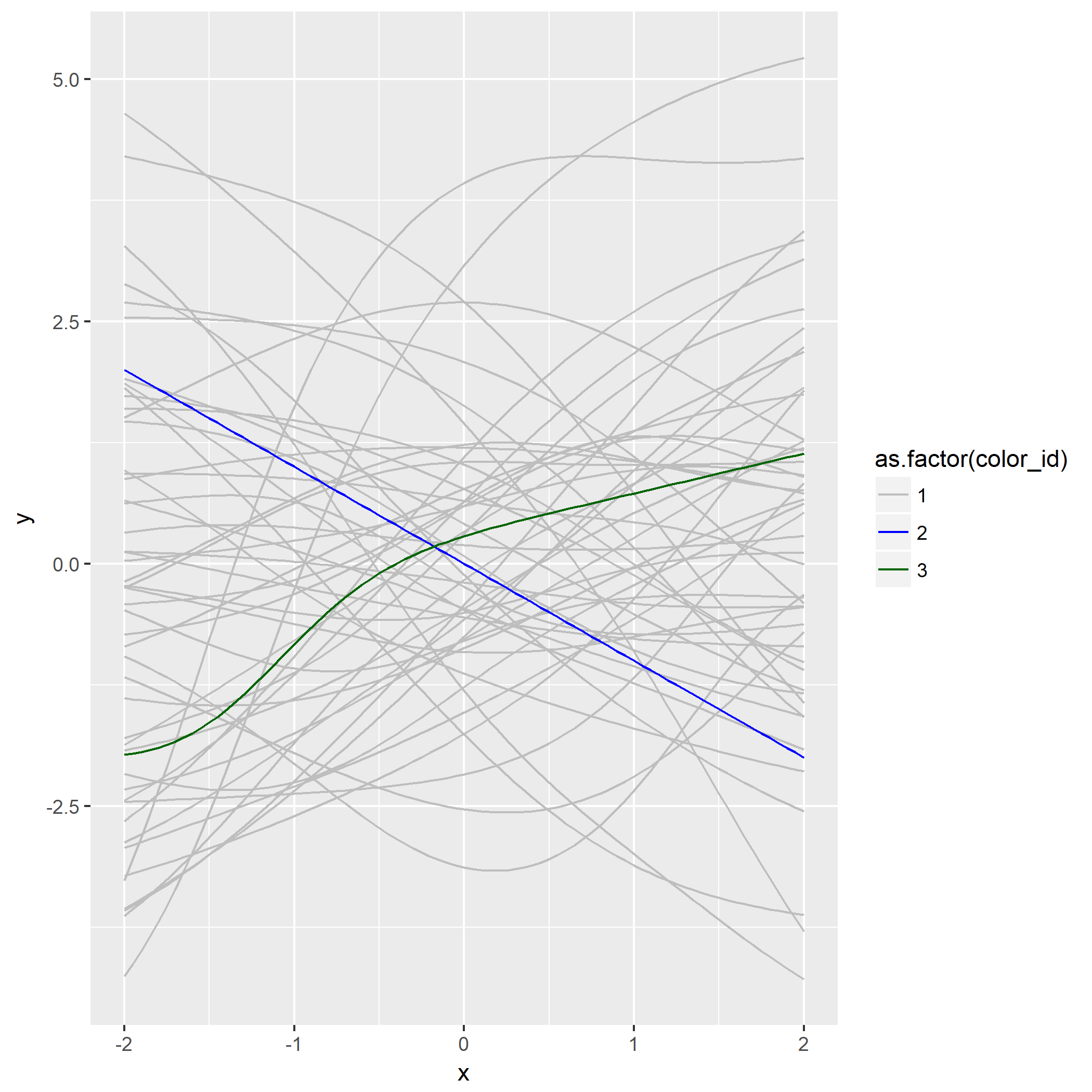
显然比第一问生成的曲线群平滑一些了,第三问当然是问观察到了什么,画一条
可以观察到误差最小时的曲线与