题目3.1 - 误差逆向传播公式推导
设
其中:
第一问求证:
这些符号里面的上下标太让人眼花了,笔者首先用其他符号代表一下:
那么条件就变成了:
问题就变成了:
开始求解:
证之。
第二问,有如下函数:
其中
这个求导基本上就是在考本科学过的求导知识,同样先简化符号
证之。
结合前两问,证明:
其中
这里的符号一样混乱,但是在简化符号代表之前首先展开并理清:
因为机器学习里面的一般方法就是设定一个误差函数,然后使得误差函数最小化,其中一个重要的方法就是求导,通过导数找到极小值点。
理解这样的展开技巧是很有必要的,因为这里是一层(隐藏层到输出层)的求导,稍后误差函数关于输入层的权重的偏导数也要进行类似的展开。
根据上式以及第一问求得的
而函数
简化表示为
剩下的
注意到:
其中
故可以求得:
所以:
证之。
题目3.2 - MLP回归
首先先观察MLP的结构:
在前面一题得到了隐藏层的权重更新公式:
在开始求解问题之前,需要得知输入层的更新公式,仿照上一题的推导过程,有:
$$
\begin{align}
\frac{\partial e^{(\alpha)}}{\partial w_{ji}^{10}} & = \frac{\partial e^{(\alpha)}}{\partial y(x^{(\alpha)}; w)} \frac{\partial y(x^{(\alpha)}; w)}{\partial h_1^2} \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = \frac{y(x^{(\alpha)}; w) - y_T^{(\alpha)}}{y(x^{(\alpha)}; w)(1 - y(x^{(\alpha)}; w))} y(x^{(\alpha)}; w)(1-y(x^{(\alpha)}; w)) \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] w^{21}{1j} f’(h_j^1) \frac{\partial h_j^1}{\partial w{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] \sum_{j=1}{w^{21}_{1j} S_j^1[1 - S_j^1]} x^{(\alpha)}_i
\end{align}
$$
其中
而:
$$
\frac{\partial h_1^2}{\partial S_j^1} = (w^{21}{1j} S_j^1 + \mathbf{bias})’ = w^{21}{1j}
$$
隐藏层的输出为Sigmoid为激活函数,于是有:
对于输入层,显然:
事实上对于题目的一层隐藏层,这样推导出来的误差逆传播公式基本上算是解决了问题了,若是有更多的隐藏层,无非就是根据这样的链式法则从最终输出层推导到输入层而已。
介绍完要用到的公式,那么就开始解题。
题目是构建一个单层隐藏层的MLP,使用tanh函数作为转移函数,拟合
笔者偷了个懒,把MLP按照如下结构构建:
将细节完整表示:
这个时候,输入层的权重更新公式变为:
各部分更新值传递在网络中的体现:
事实上到了这里,我们基本上算是解决了这个问题,剩下的就是具体编码了,笔者的实现在Github
解题所使用的数据集
第一问是输出训练过程中误差变化:
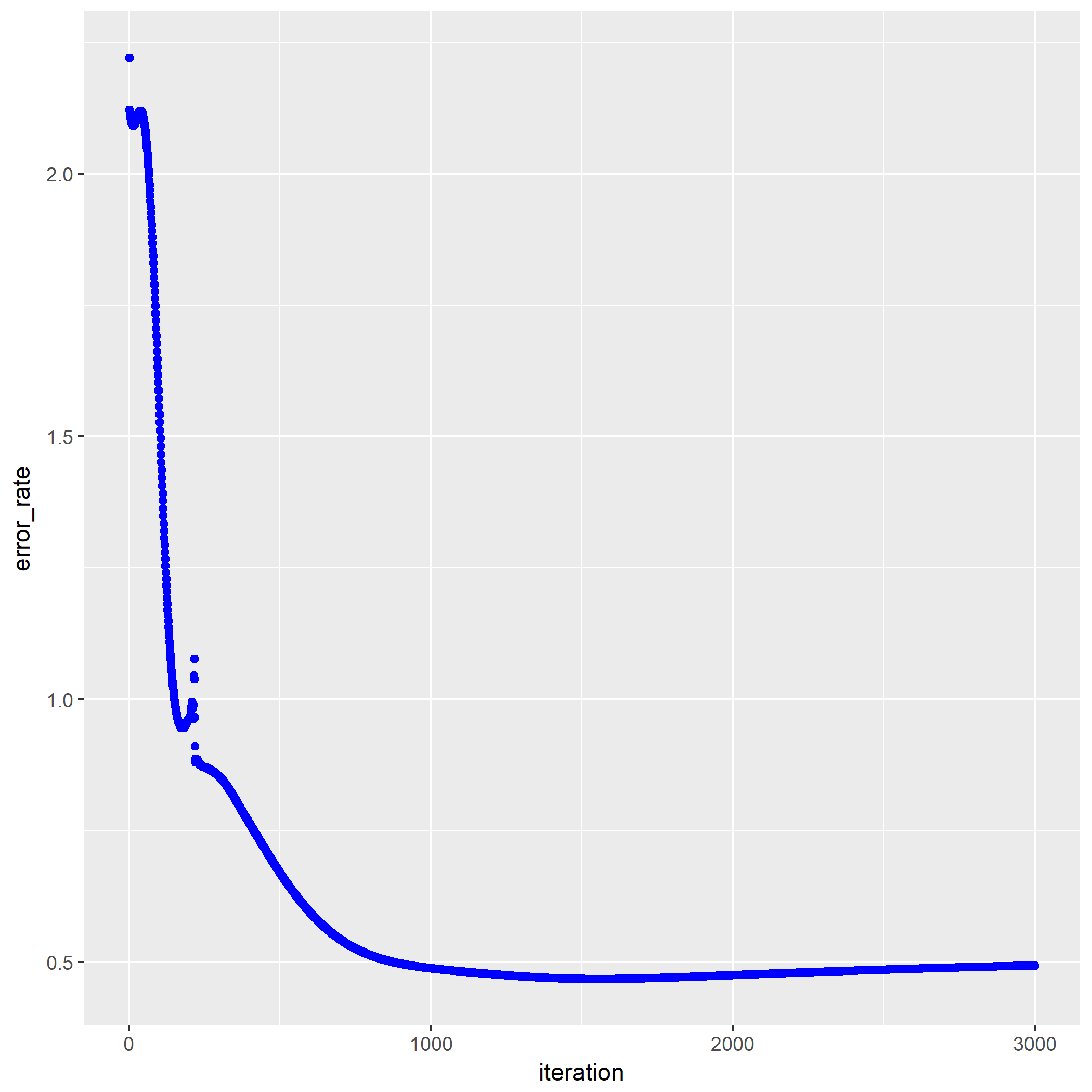
可以看到笔者用了3000次迭代。
第二问是画出训练后3个隐藏层各自的输出:
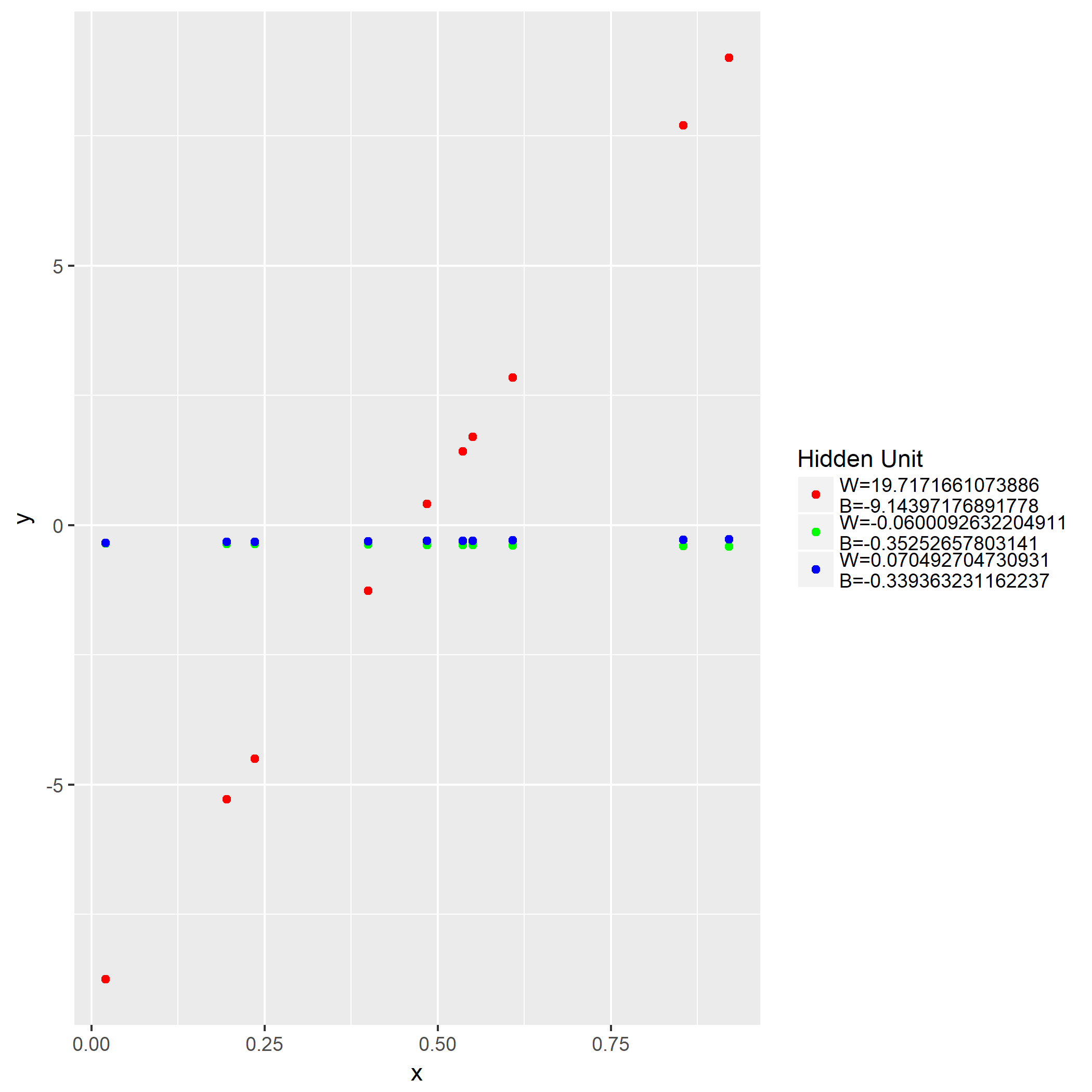
第三问是画出训练用的输出以及训练好的网络对于样本的输出:
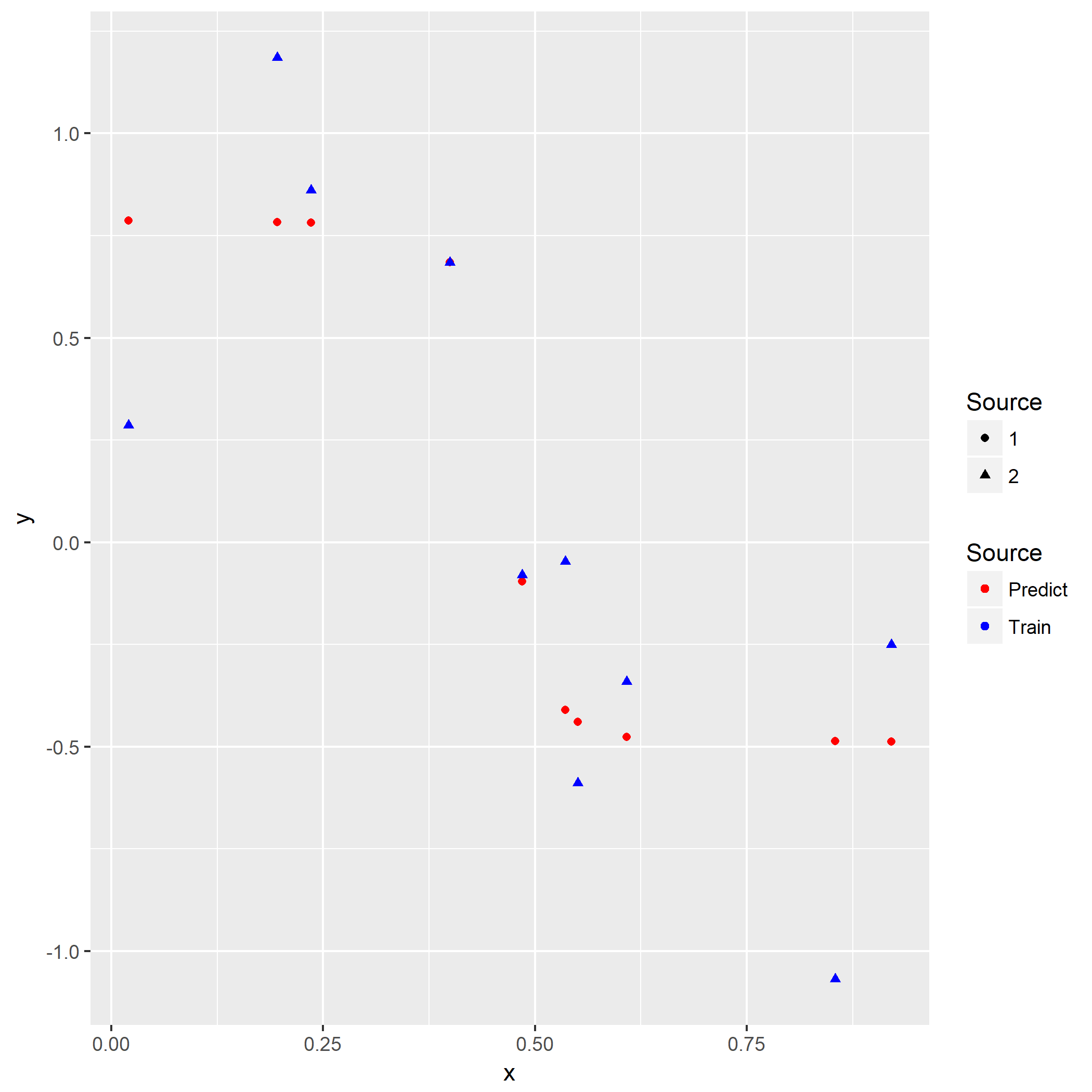
至于最后两问仅仅是把上面三问重复一边,对比差异,以及解释差异而已。
至此本节的解题结束。