机器学习练习笔记(四)

题目4.1 - 线性搜索

考察一般梯度下降用的更新公式：

第一问是用2阶泰勒对任意在的近似展开。

于是根据定义式有：

第二问是利用上述推导式以及不等式推导步长的上下界。

$$
\begin{align}
E^T(w_{t+1}) & \leq E^T(w_t) \
E^T(w_t) - \eta_t d_t \nabla E^T(w_t) + \eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq E^T(w_t) \

\eta_t d_t \nabla E^T(w_t) + \eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq 0 \
\eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq \eta_t d_t \nabla E^T(w_t)
\end{align}
$$

不等式至此需要分情况讨论了。

当时，有且仅有；

令符号，则有：

当或时，；

当时，为大于零任意值。

第三问通过求解当前权值下最优步长。

首先查看二阶泰勒展开式：

根据链式法则有：

而：

可得：

另外：

所以：

令算式等于0即可解得的表达式。

最后一问是证步长与搜索方向正交，这题笔者真不会证了。

该题比较三种下降法：

利用公式，画出常数学习率的最速下降法权重分布图以及关于迭代变化的图：

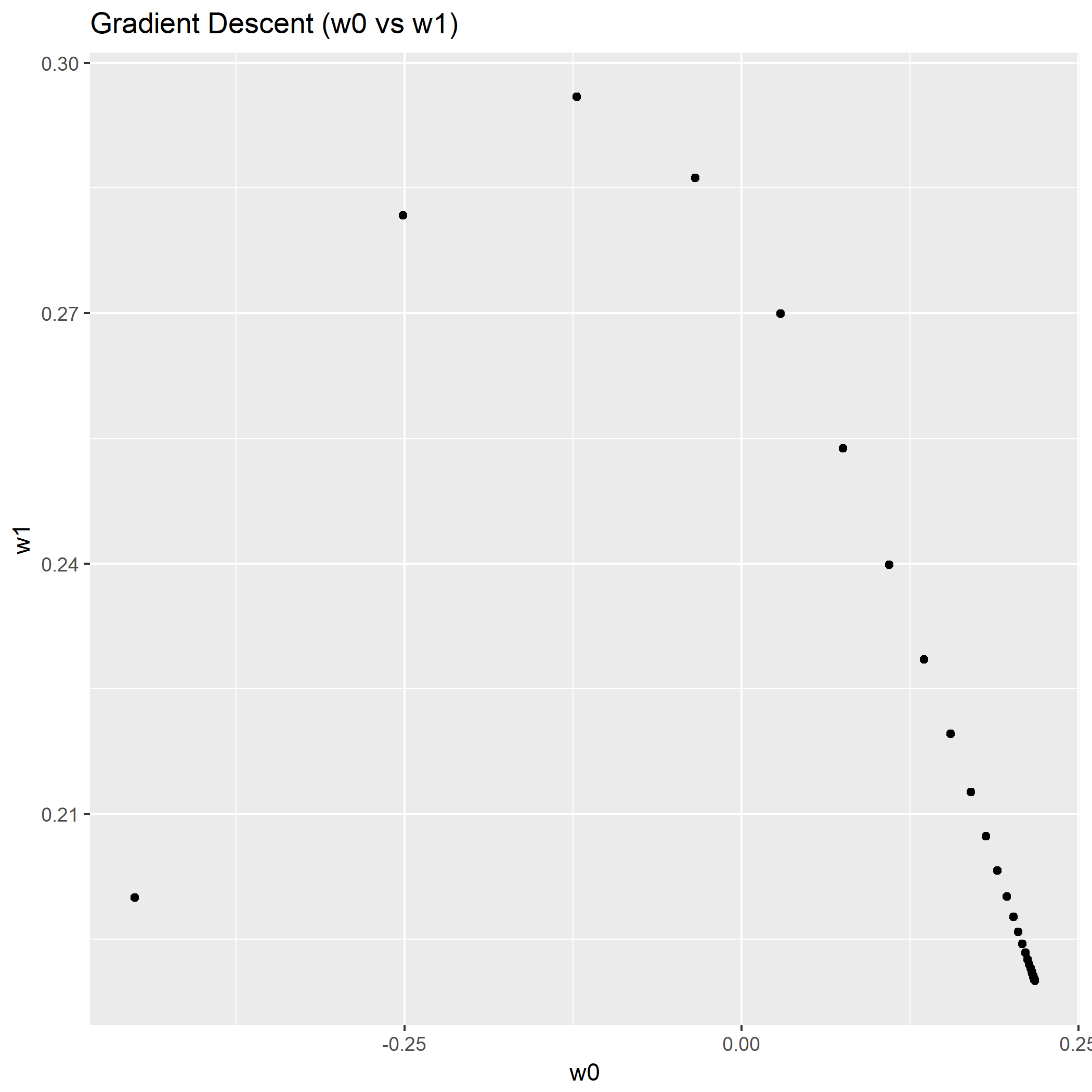
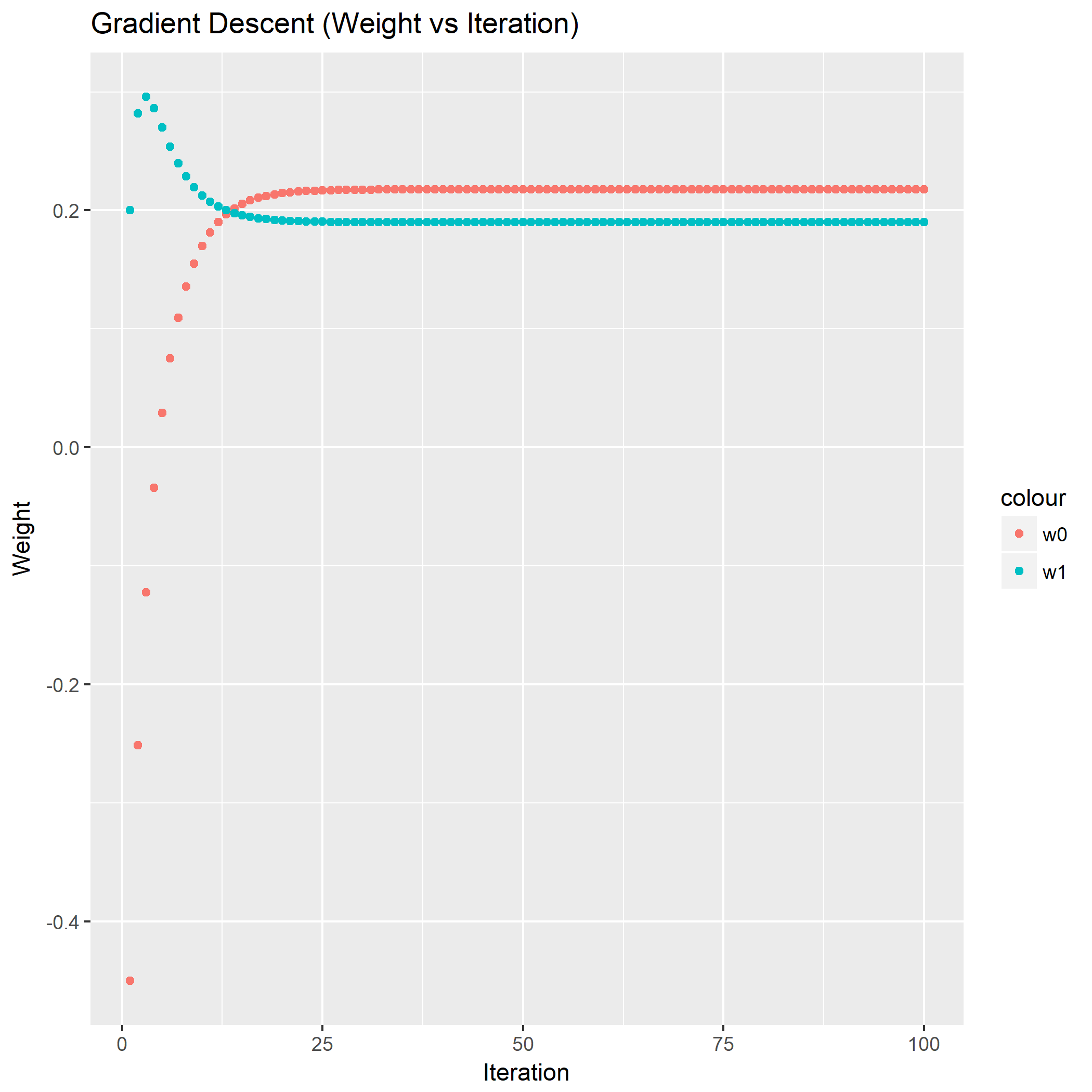
利用线性搜索的最速下降法：

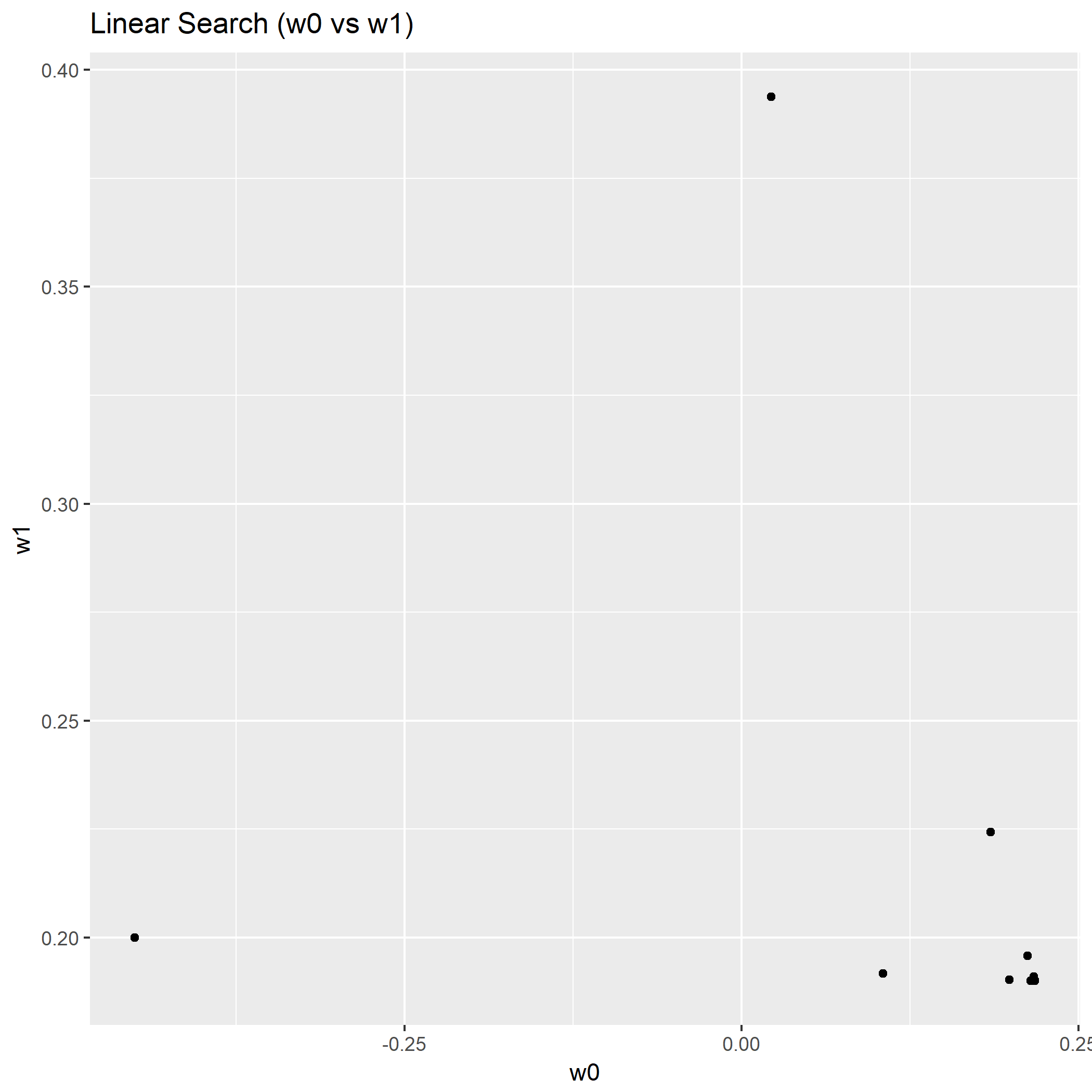
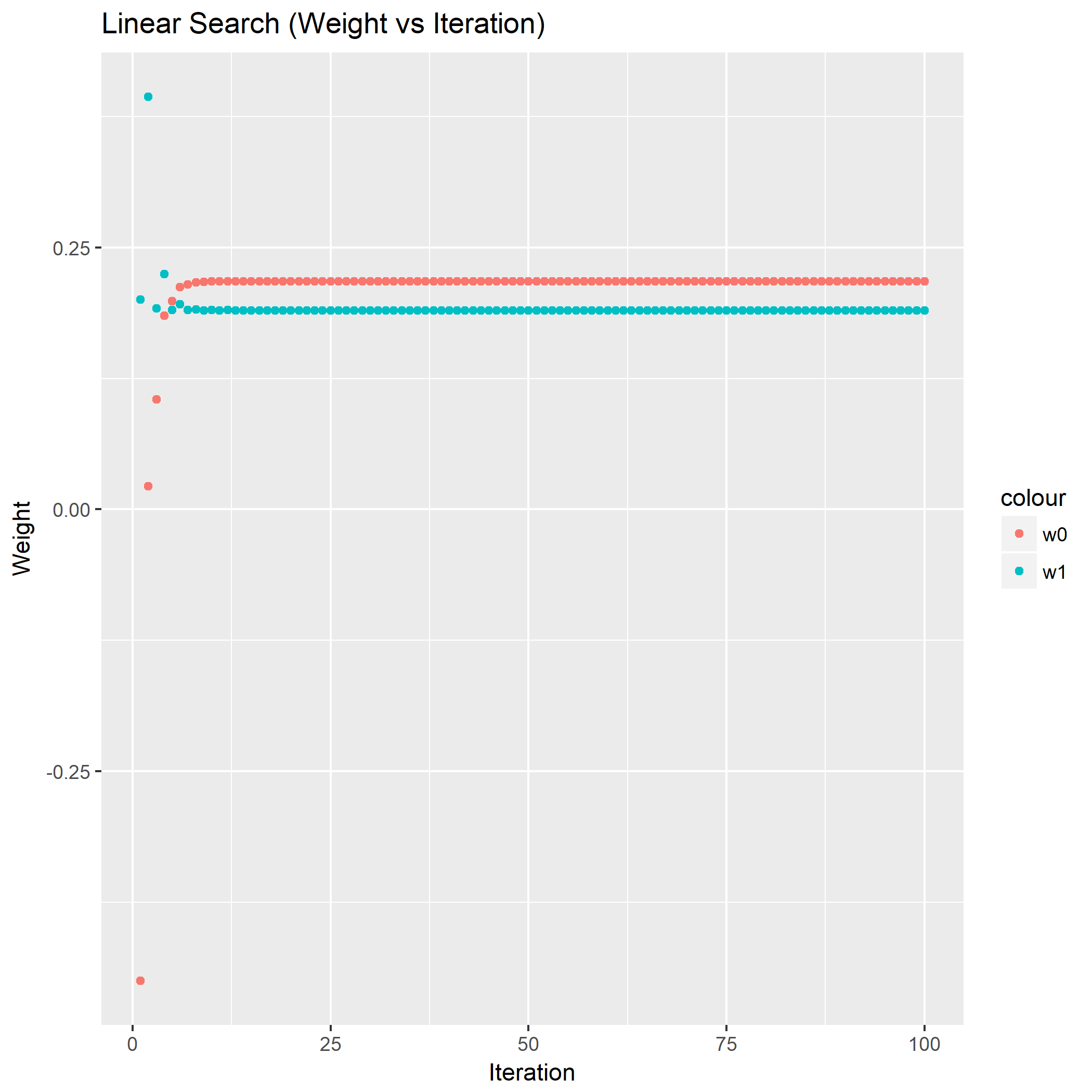
显然可以看到用了线性搜索步长的最速下降法收敛速度提升很明显，从权重分布图来看不少的点集中在的最优解附近，从关于迭代的图来看，收敛到最优解的迭代次数要少些。

剩下的共轭梯度法：

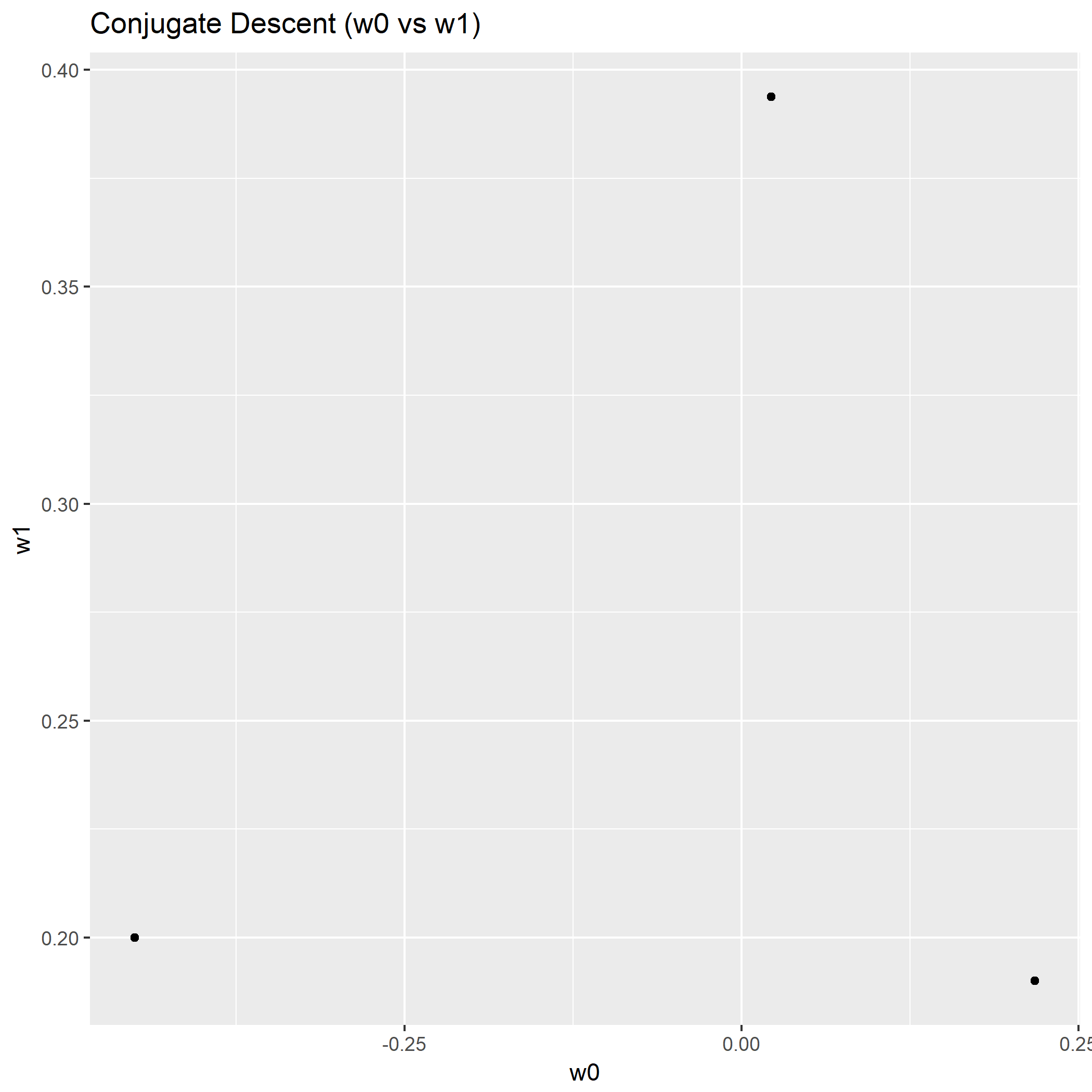
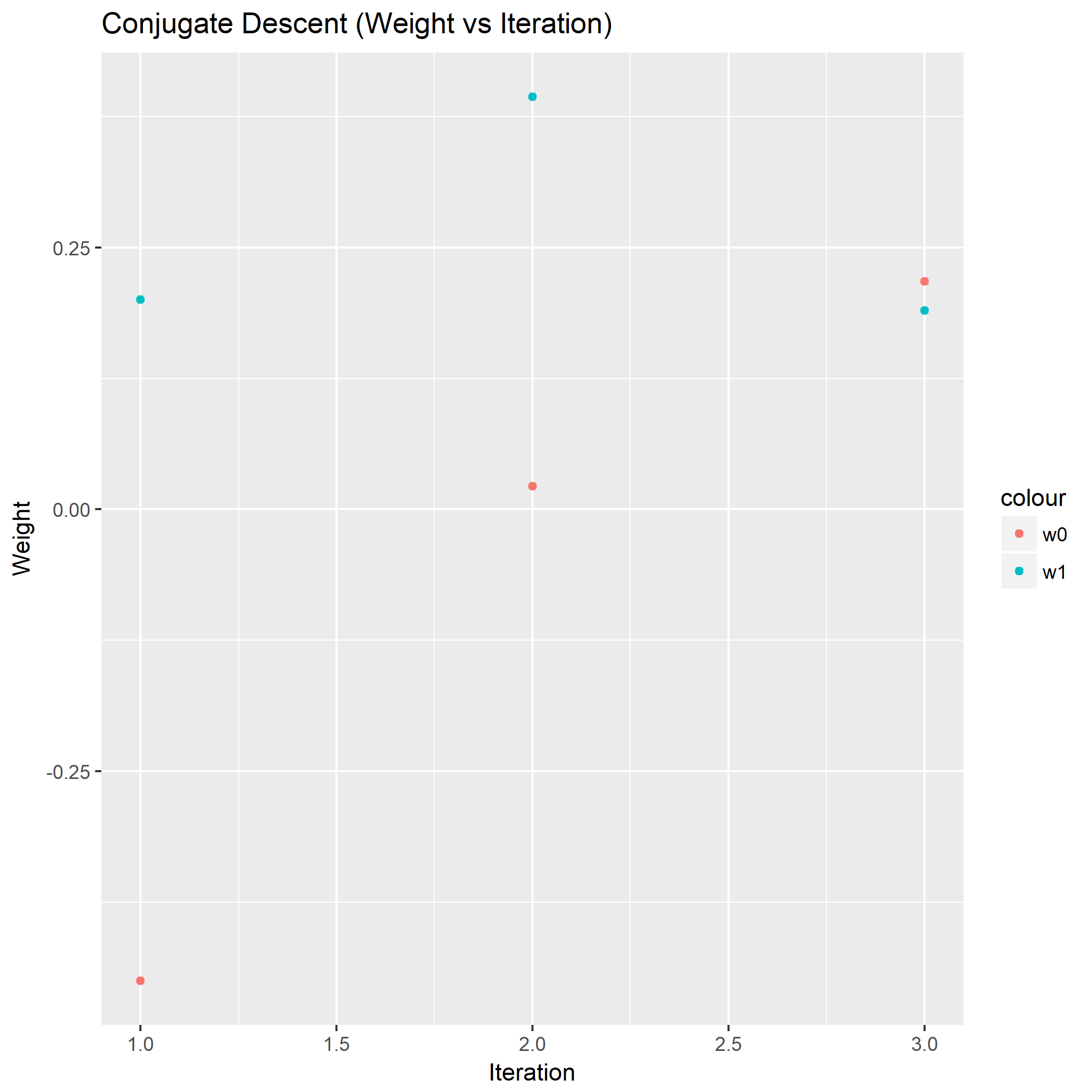
虽然设定了最大迭代次数为100，然而共轭梯度法收敛到最优解之后，就不会产生合法的更新值了，所以第三轮迭代以后算不出步长，只能强制在收敛时结束迭代。

由此对比，共轭梯度法取得了最好的表现。

至此，第四节的问题解决。