该章里面涉及一个白化的概念。
在解本章题目之后,笔者认为除了算法实现之外的全部知识属于线性代数以及坐标变换,虽然题目要求与PCA算法有些不一样,但是其涉及到的线性代数知识是共享的,故理解白化过程之后,就很容易理解PCA了。
题目5.1 - 交叉验证
所用的训练集:
- 200个样本
,其中 。
以及验证集:
- 1476个样本
,其中 为坐落在 图像的坐标信息。
第一问是将训练集以及验证集的数据白化后作图,首先画出白化前的数据分布:
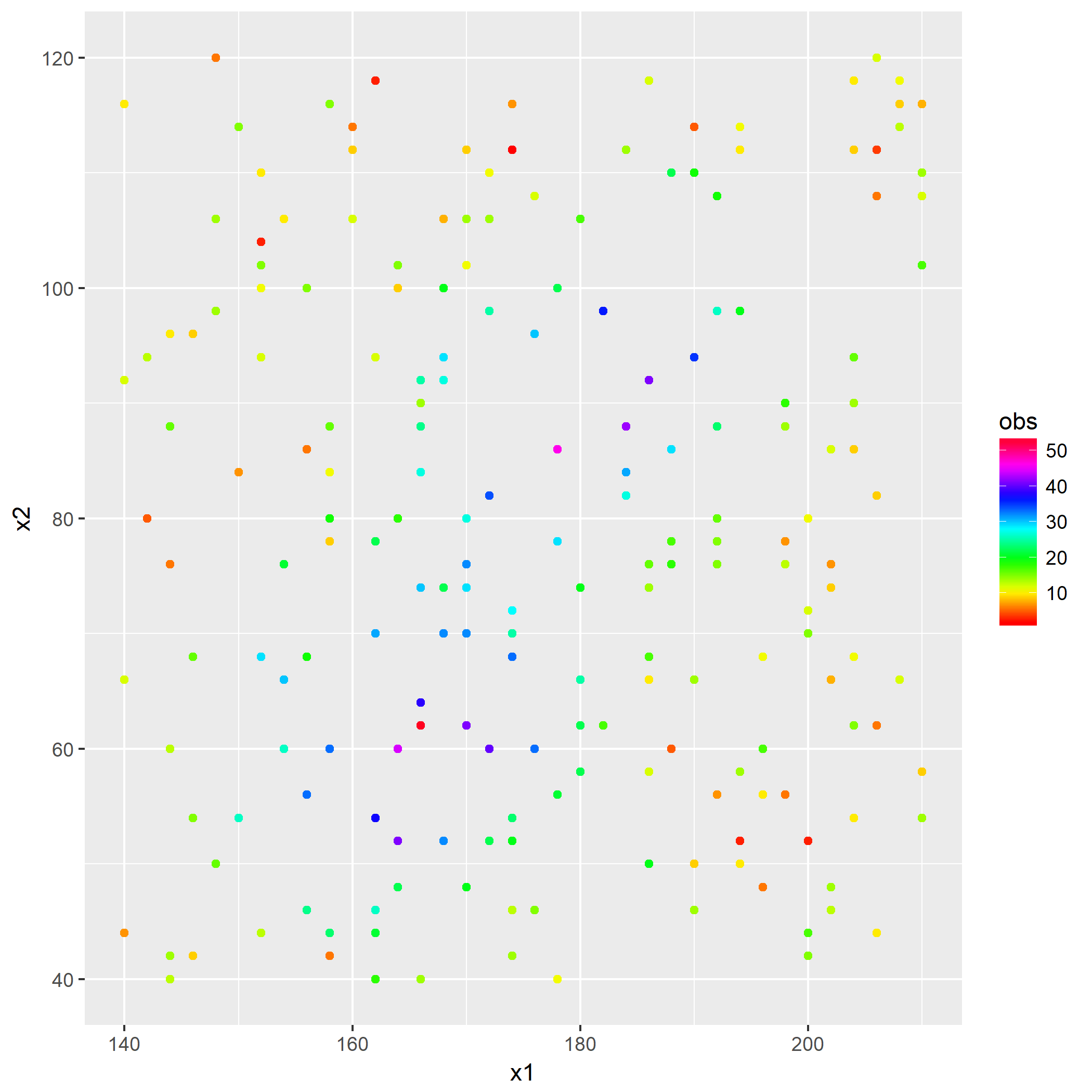
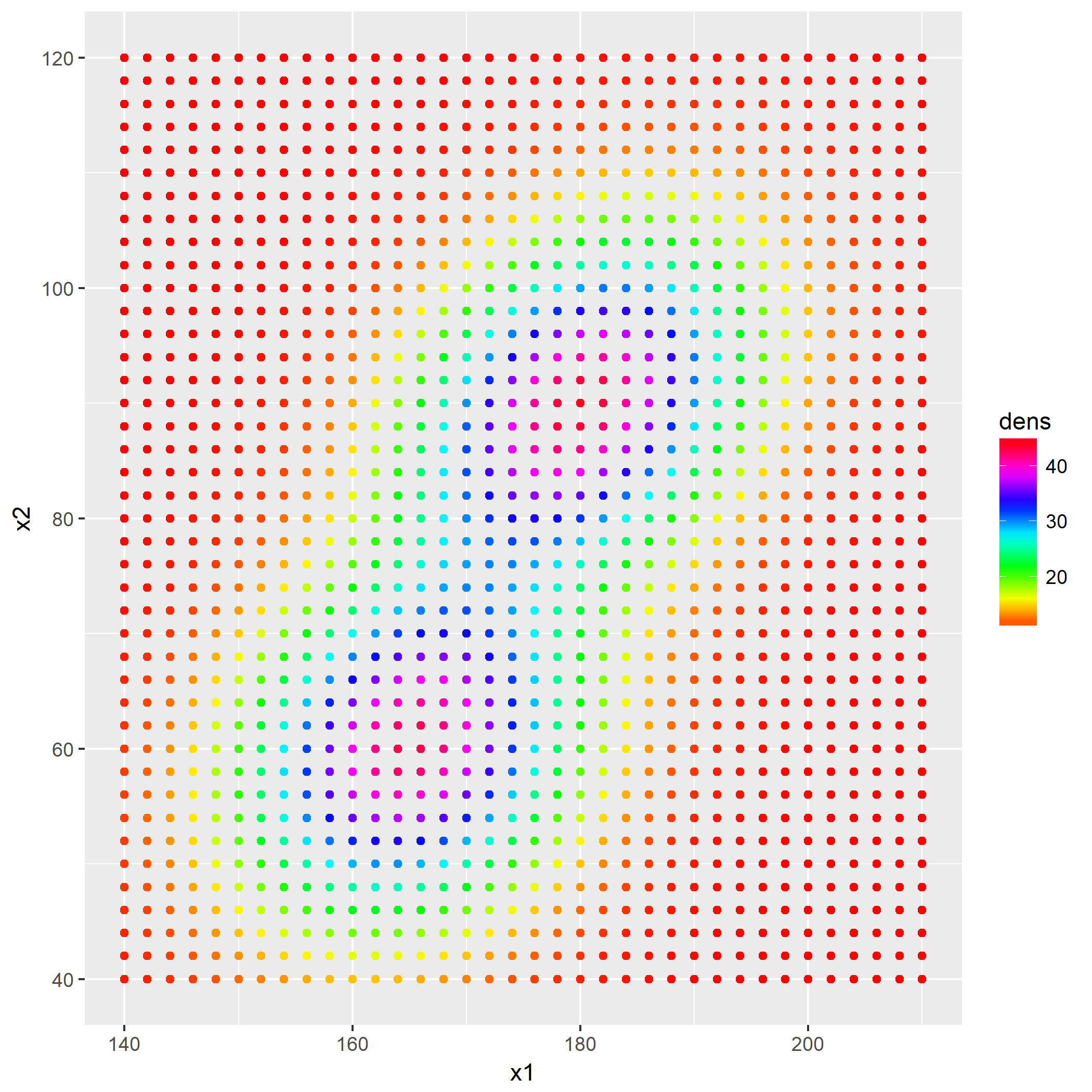
在开始解题前已经介绍过白化过程了,于是直接贴出白化后的数据分布:
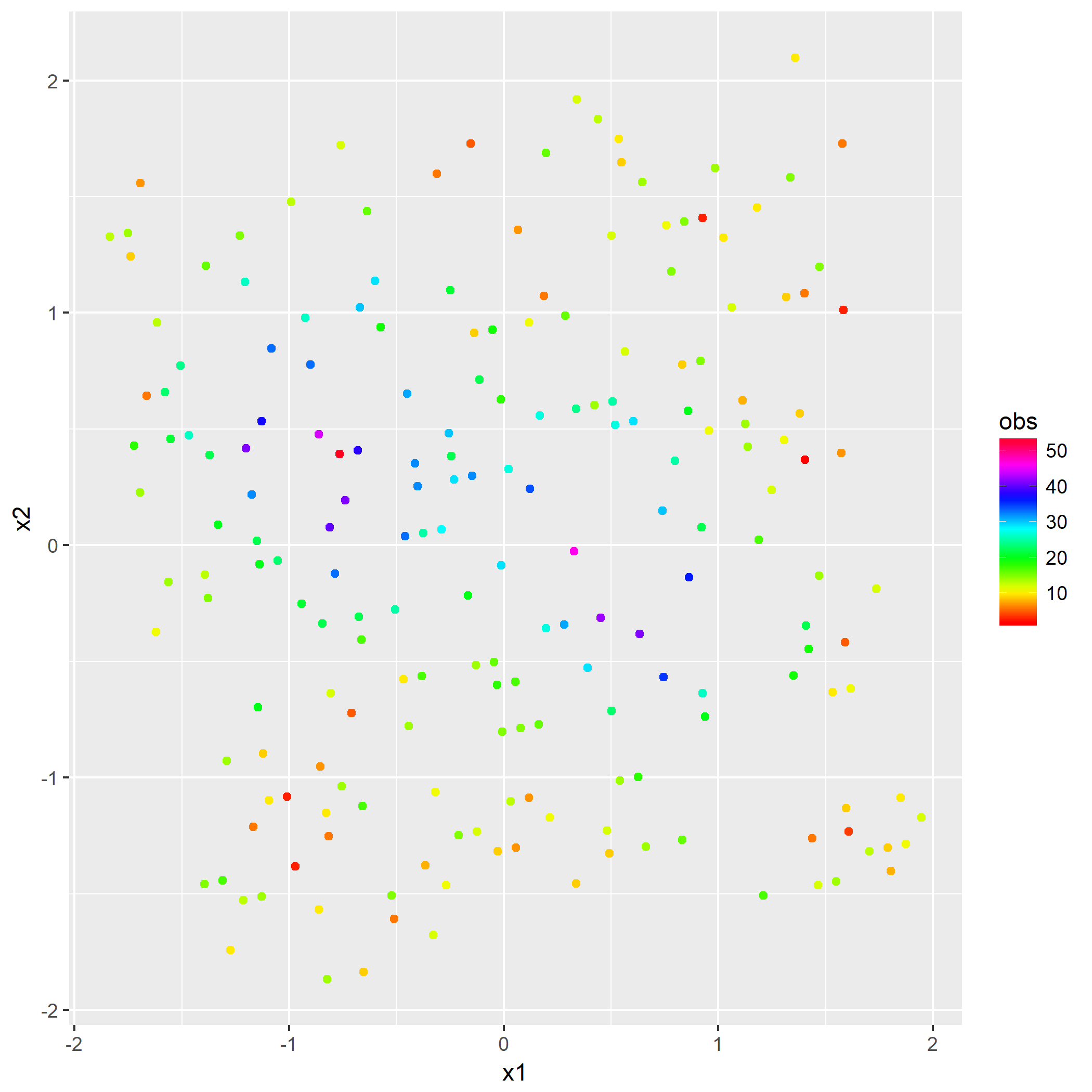
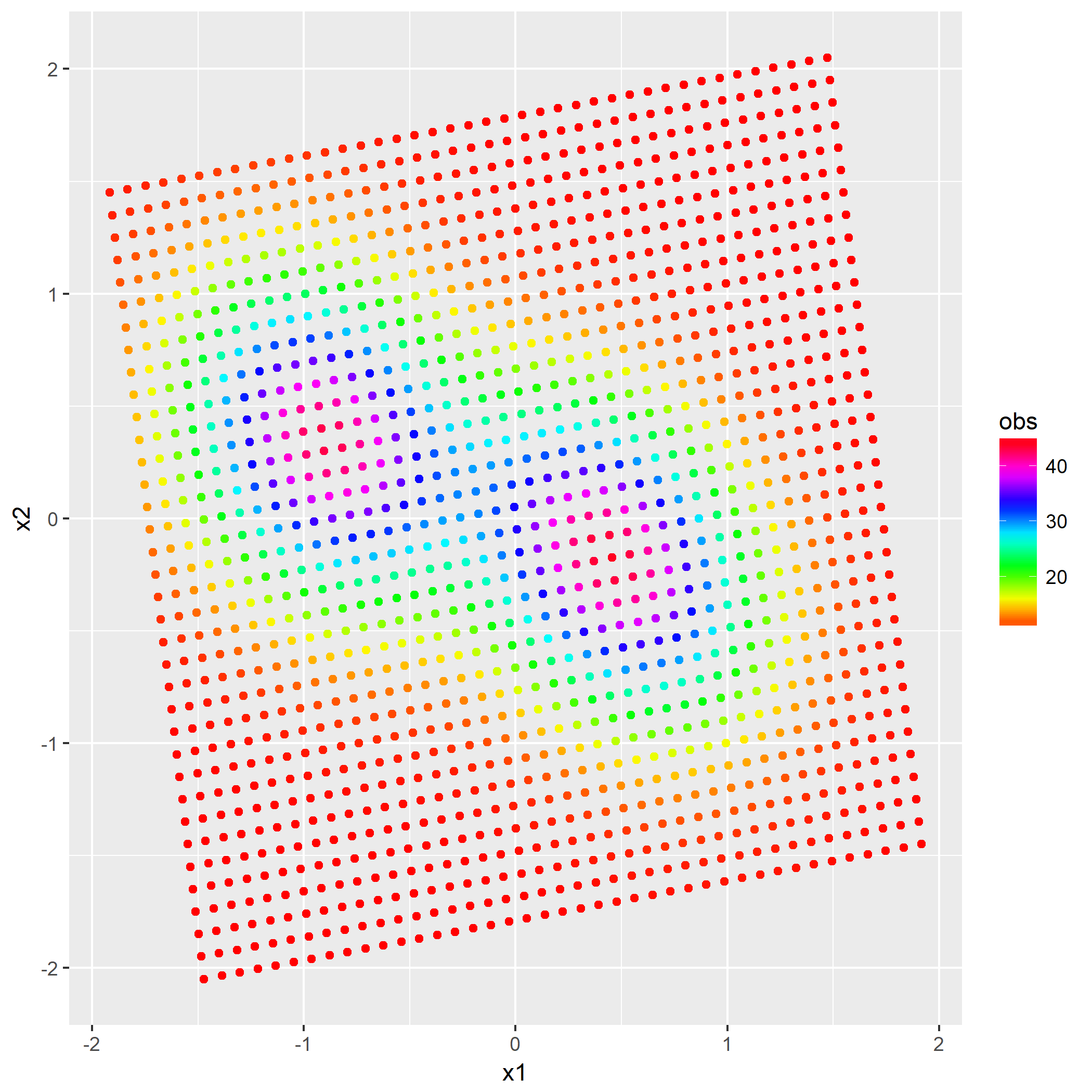
第二问是多项式展开,利用核函数将白化后的数据从2维升至更高维度,使得非线性问题在高维表示为线性问题。
所用的映射函数:
例如当55项这样的单项式,根据该映射函数,所用的预测方程为:
而
然而本题要输出的是各单项式的值,例如当
笔者懒得去画了,毕竟用ggplot将多张图片放在一个输出文件中有点麻烦,读者可以挑其中一个,如
其中
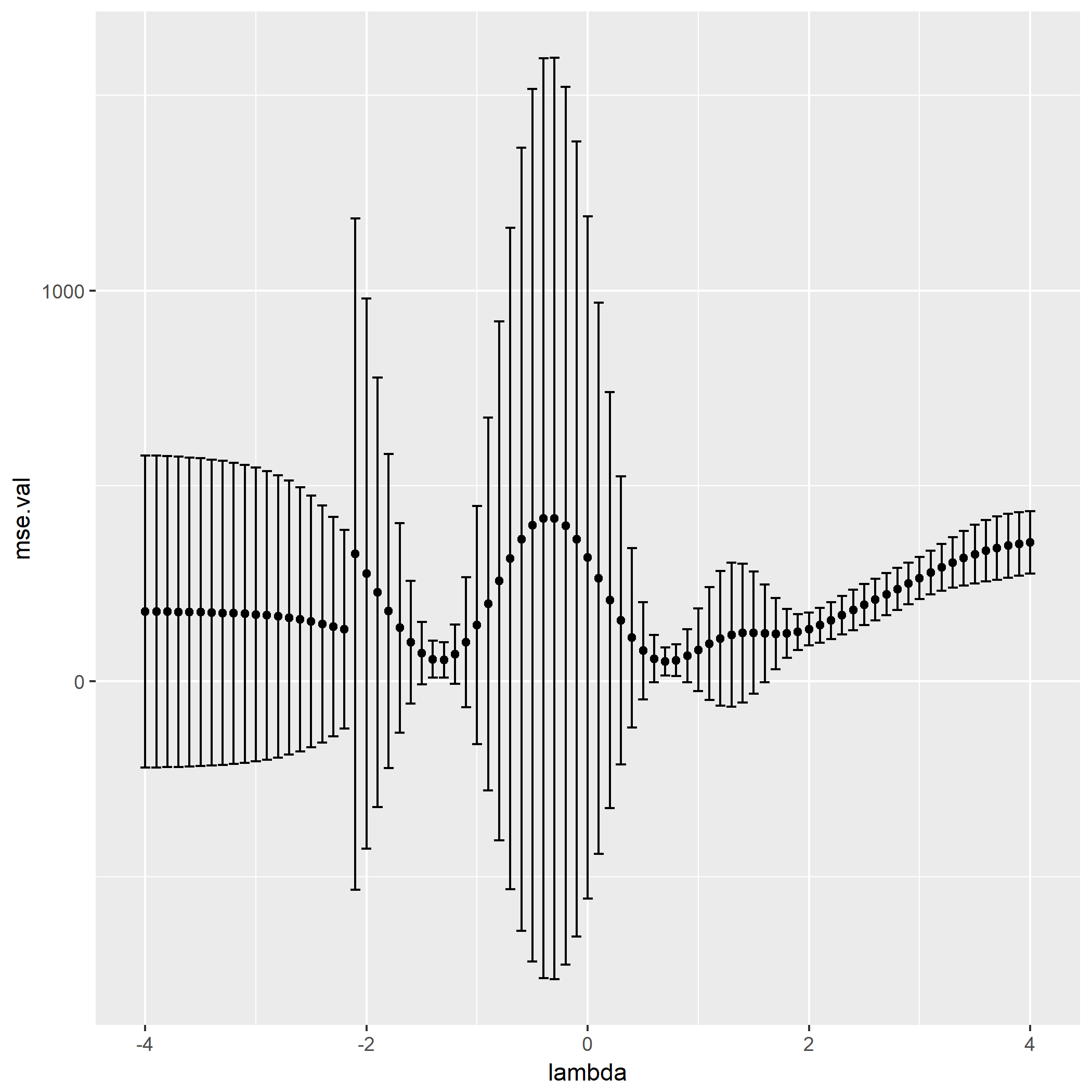
可以看到
最后一问是试出对于验证集最好的
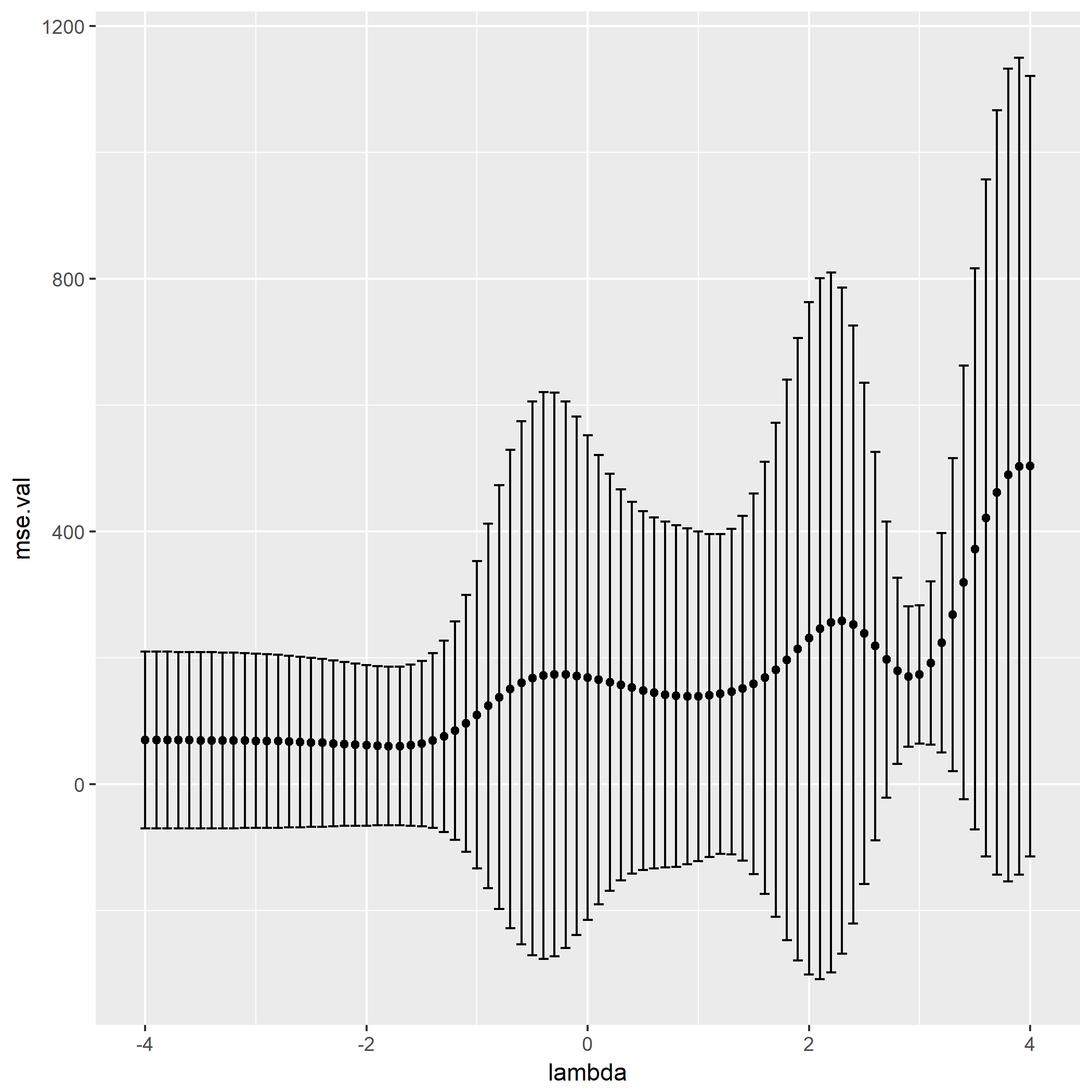
然后最佳的
至此第五章题解完毕。