矩阵运算与坐标变换

相信本科时候没有好好学线性代数的同学会对：

$$
\left[

\right]
\left[

\right]

\left[

\right]
$$

这样的一个矩阵乘法之后，原坐标下的向量坐标就会变成了新坐标下的向量坐标，多少会感觉到一些突然。

笔者在此复习一边这样的矩阵乘法与坐标变换的关系。

好了，从熟悉坐标系开始，假设我们在这个坐标下有一个向量：

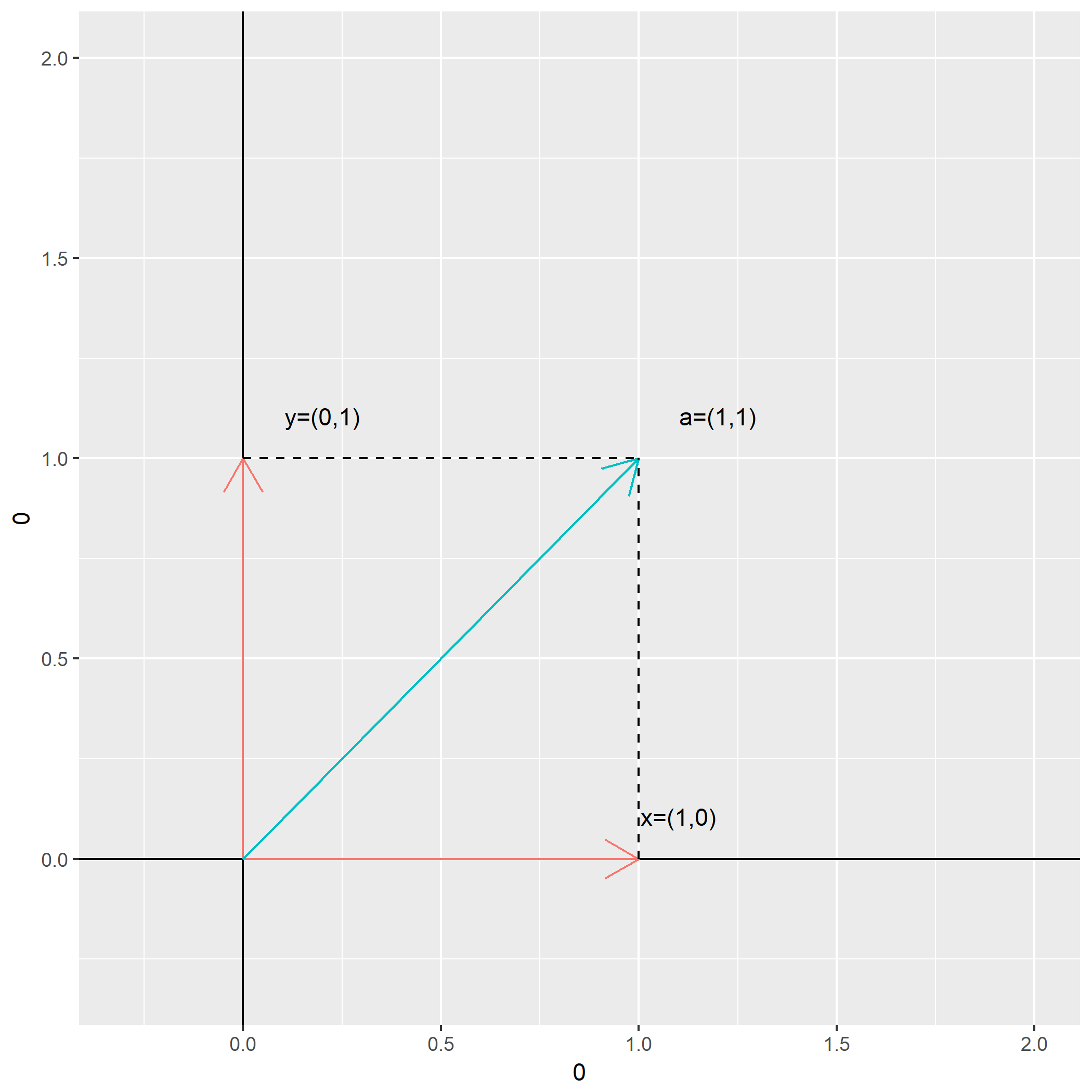
事实上图中的坐标系是由一组标准正交基和构成的。计算一个向量在一组基下的坐标是分别用该向量与每个基作点乘（投影），得到向量在每个基下的投影长度。

例如计算就是分别计算与的值。

那么将向量的形式换成用线性代数一般的表示形式：

那么坐标系变换的过程可以表示为如下的矩阵运算：

$$
\left[

\right]
\left[

\right]

\left[

\right]
\left[

\right]

\left[

\right]
$$

矩阵运算与坐标变换就这样联系起来了，当然这里全都设置为的值，当然看不出变换在哪里了，这里开始从原来的组成的坐标系开始作变换：

假设有一组新的标准正交基，容易验证：

新标准正交基加入后，作图如下：

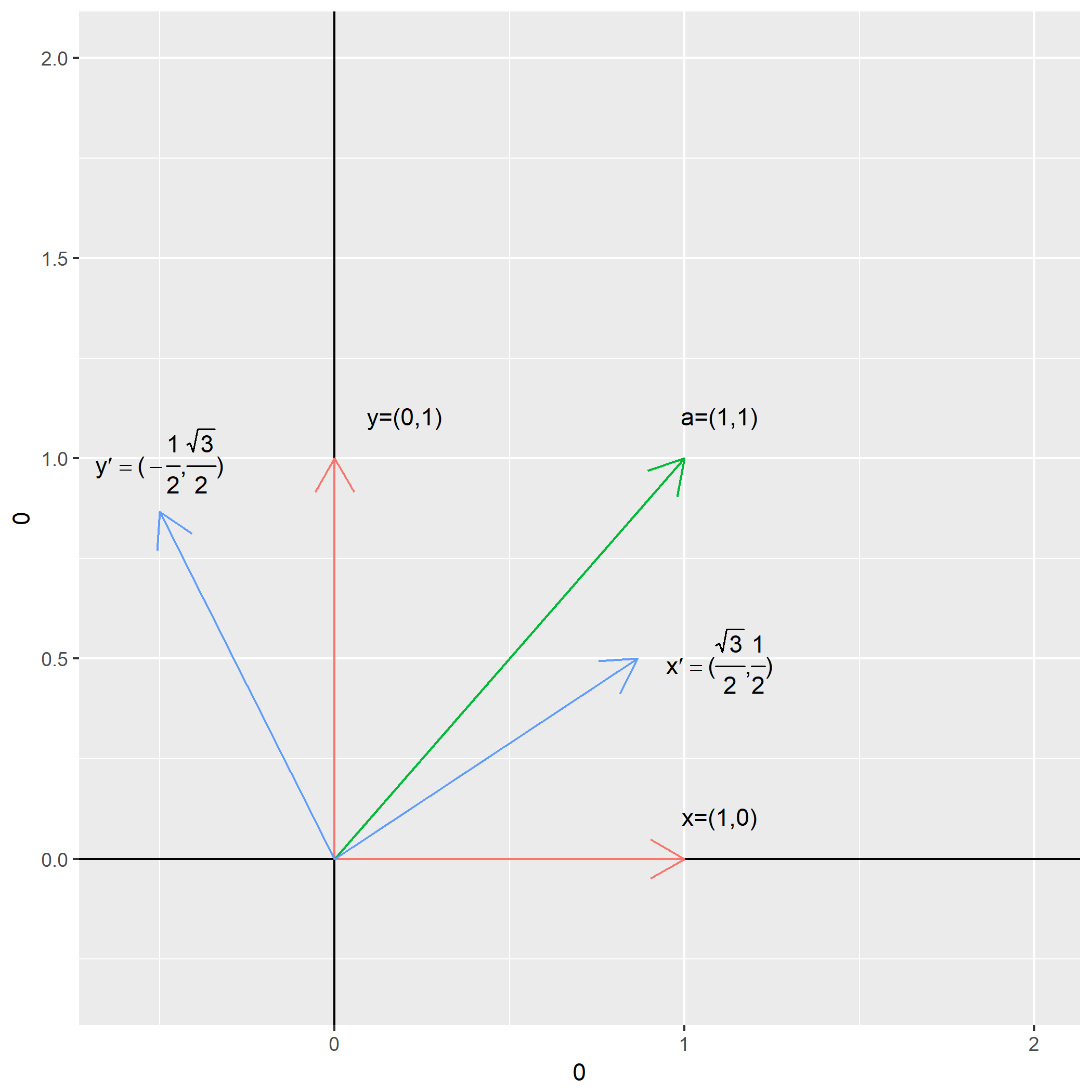
计算原向量在新坐标系（基底）下的坐标（各基底下的投影长度）如下：

写成矩阵表示：

$$
\left[

\right]
\vec{a}^T

\left[

\right]
\left[

\right]

\left[

\right]
$$

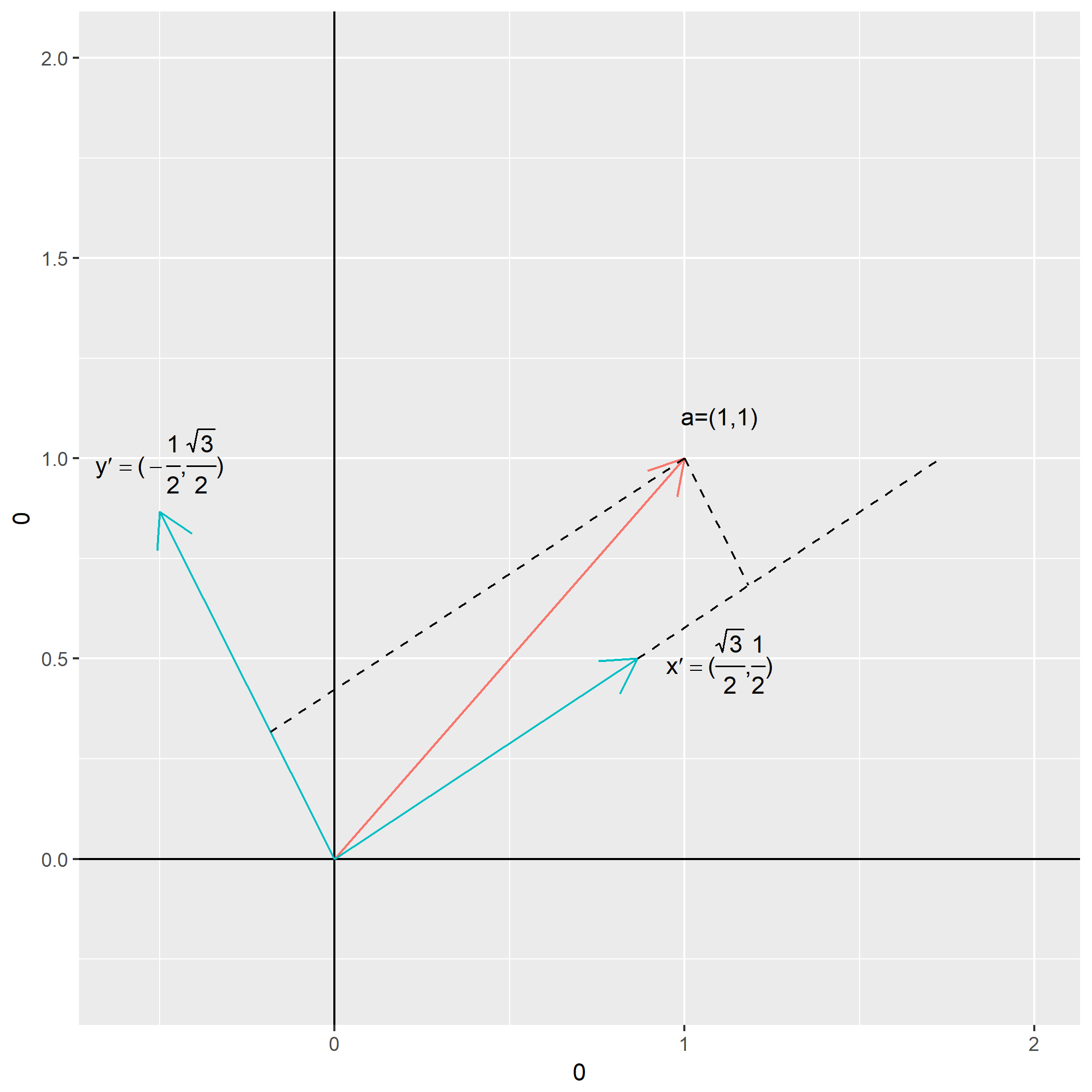
抹去原来的坐标线，只看新基底与被投影的向量：

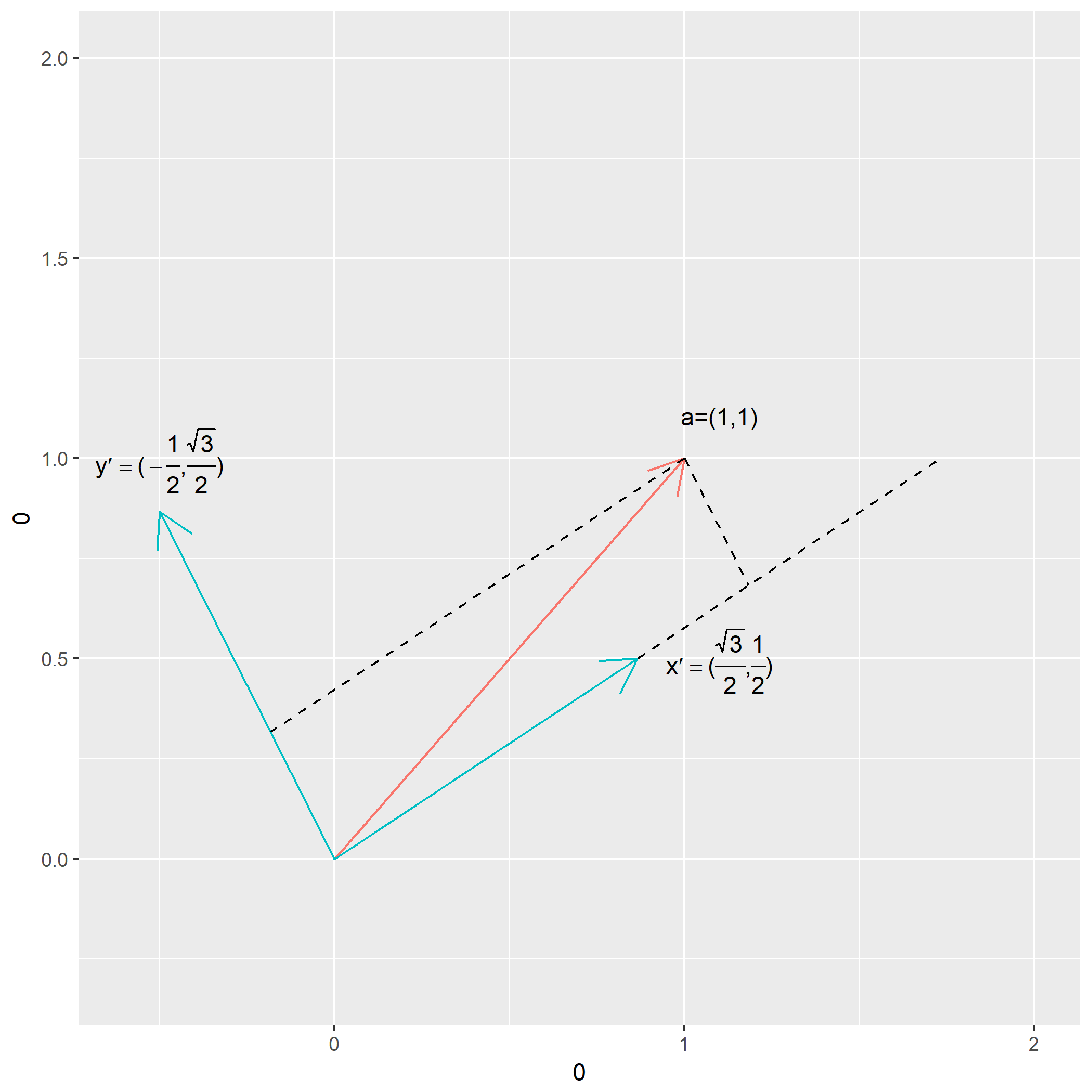
把头倾斜一下，就看到形成的新坐标系：

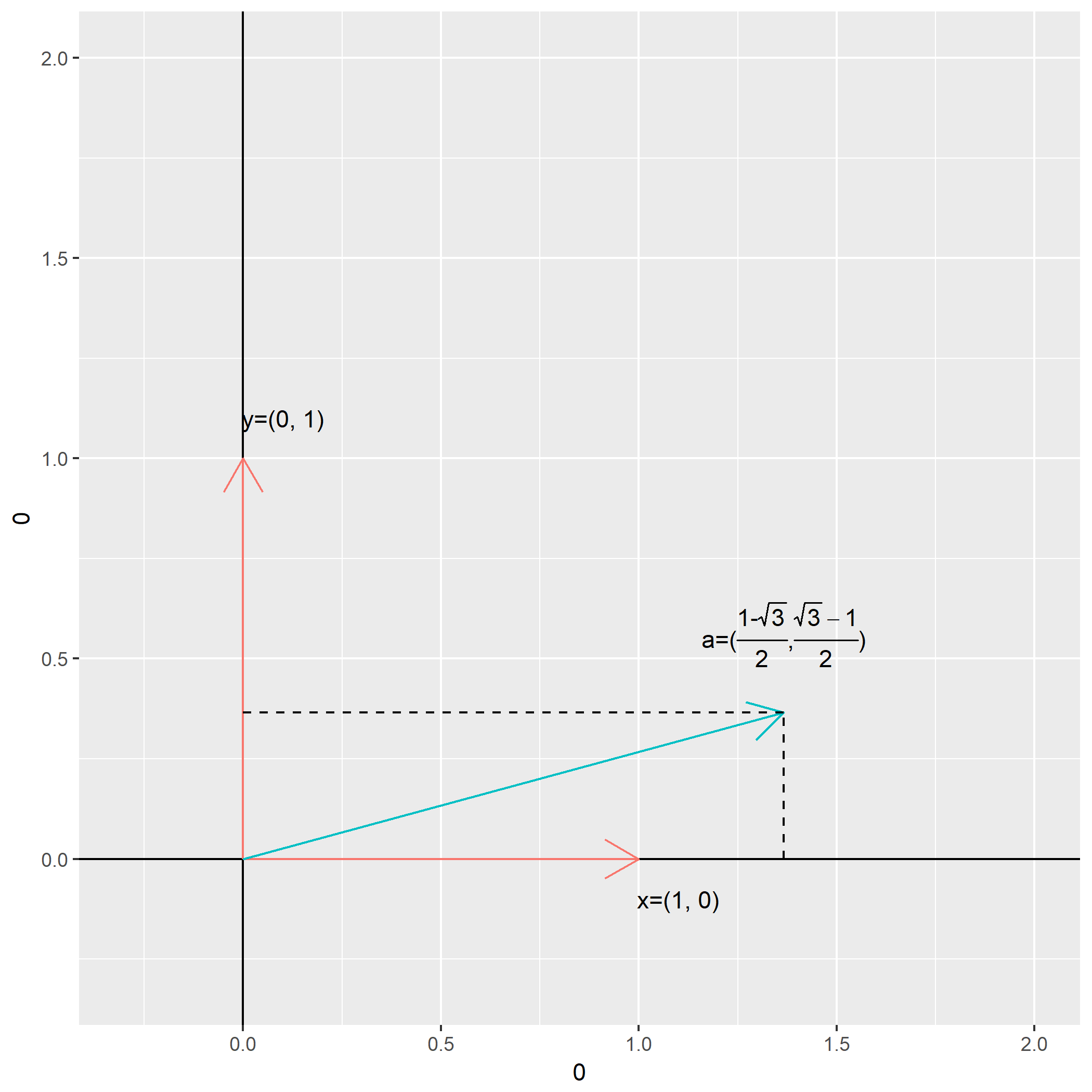
注意新基底在变成了新坐标，因为他们自己投影自己后的长度都为，并且正交，在对方的投影值都为。读者可以试试用投影定义式计算图中向量在新坐标系下的坐标值。

对于个标准正交基组成的向量空间，其坐标变换可以表示为矩阵运算：

$$
\left[

\right]
\vec{x}^T

\left[

\right]
\left[

\right]
$$

其中与为原N维空间下的坐标向量，长度为n。

当需要表示更加复杂的变换，例如2维空间下，需要平移操作，这个时候增加一维信息，具体有兴趣的读者可以到网上了解。

至此，又复习了一课线性代数。