机器学习练习笔记(八)

本章节是一些统计学习理论。

题目8.1 - Vapnik-Chervonenkis dimension，VC维

使用的定义以及二项式的递归属性：

对于，证明一个线性分类器，，其VC维。

记住，$$\tilde{C}{(N+1,N)} = 2^{N+1}\tilde{C}{(N+2,N)}<2^{N+2}$$。

显然笔者暂时不会证，或者网上已经有大堆博客，这题先放着。

题目8.2 - 分类可变性

假设样本分别属于两个聚类，分别通过正态分布，其中，是单位阵。使用N个样本，测试一个线性神经元学习出来的模型的性能如何。按照如下步骤:

1. 对于两个聚类，分别产生个数据点，当类属为时，；当，当类属为时，。
2. 根据均方误差最小化，得出。
3. 产生根据同样的分布，每个类属产生500个测试样本。
4. 分别计算经验（训练）误差以及测试误差。

对于，分别重复50次，记下训练后的参数以及训练集的精度和测试集的精度。

第一问使用误差棒图描绘出每个N下的训练精度以及测试集精度均值和标准差：

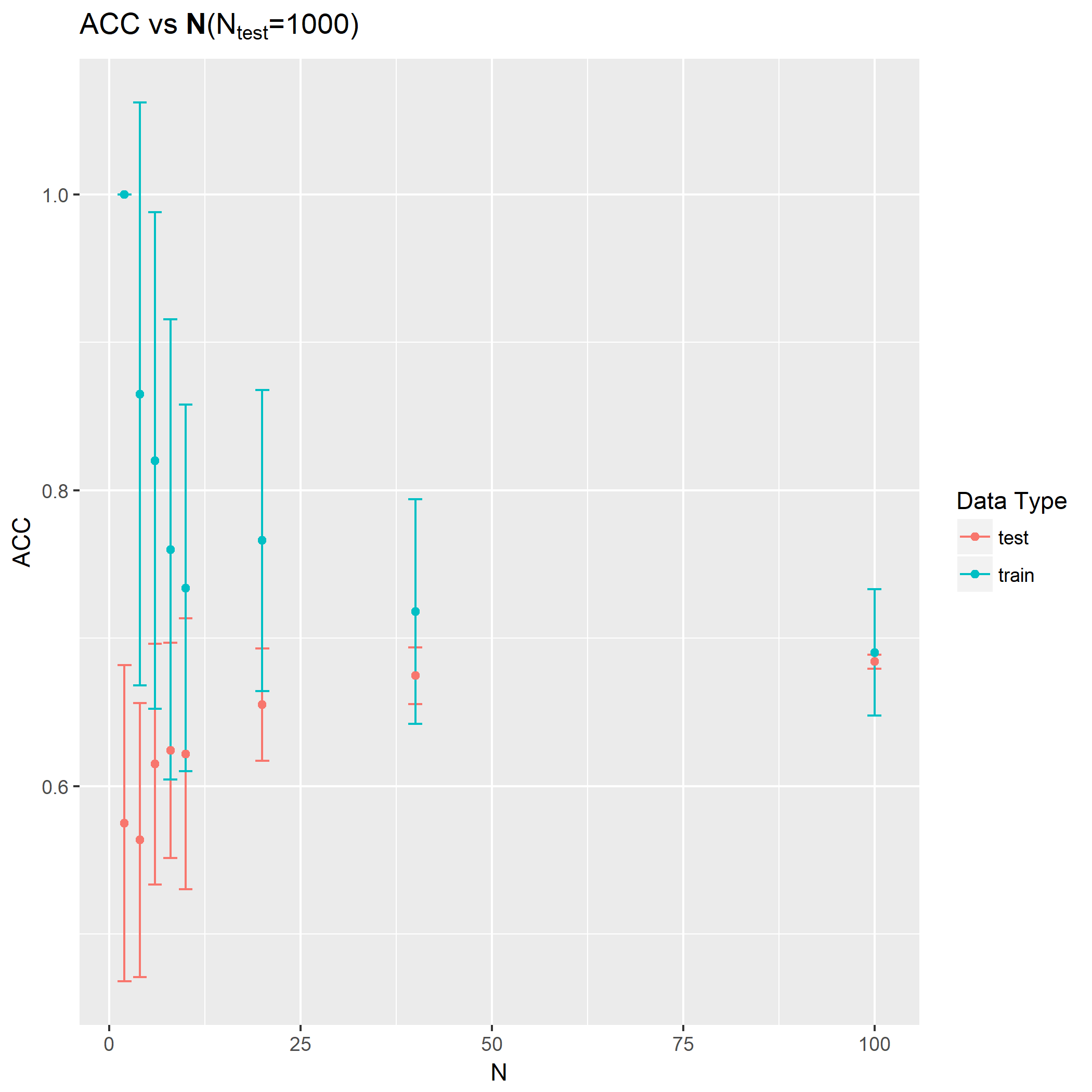
可以看到训练样本越少，模型越容易过拟合，泛化性能越差，模型也不稳定（方差大）。

第二问分别绘出关于N的误差棒图：

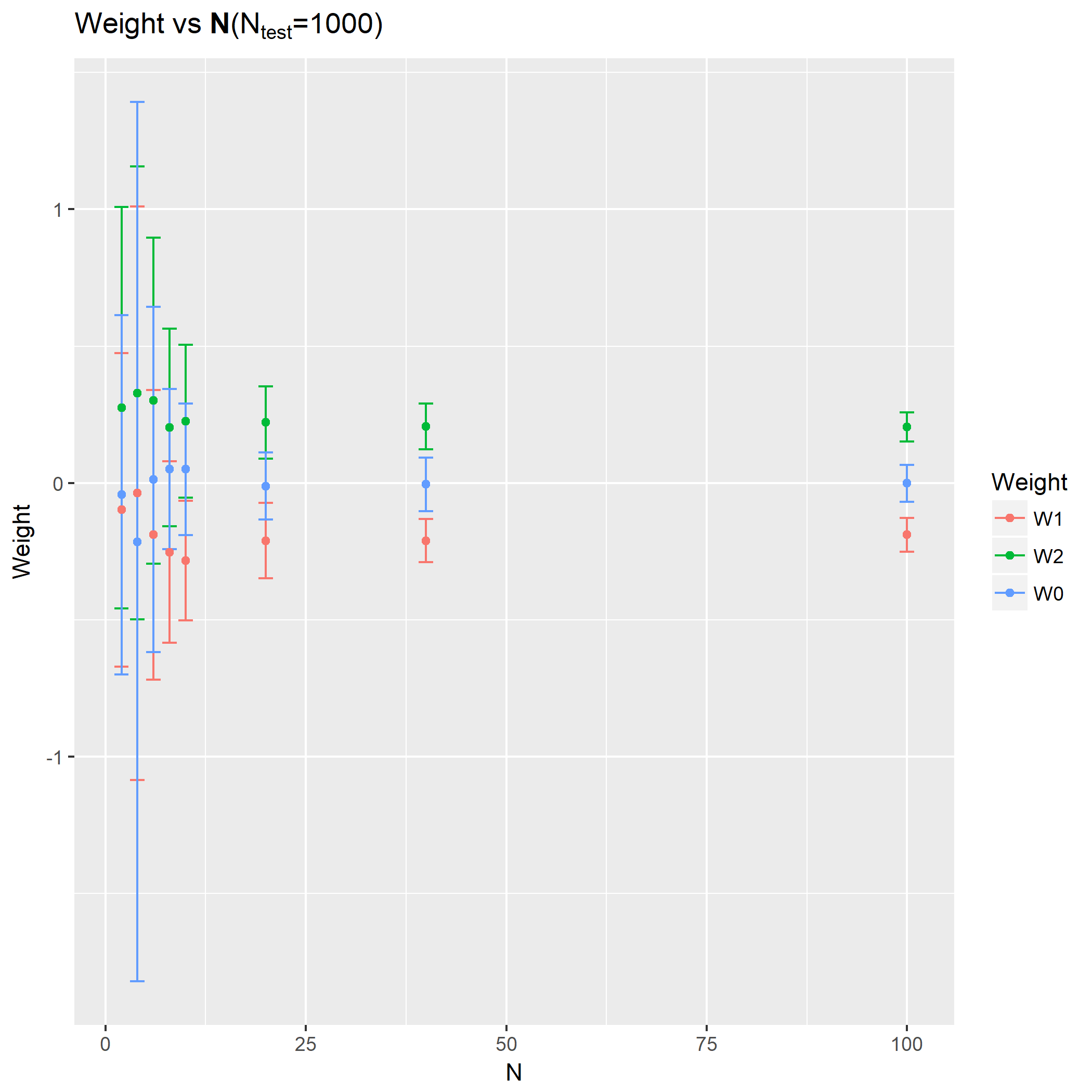
基本情况跟第一问一样，样本越少，重复中出来的参数误差越大。

题目8.3 - 二项分布

本题目涉及三个概率密度函数：

第一个问题是通过不同绘出函数图形。

第二个问题是什么条件下，可以合理使用正态分布近似二项分布。在时，正态分布可以近似表达。可以绘制一个样本图像来说明。

第三个问题是什么条件下，可以使用泊松分布来近似二项分布。当二项分布的很大而p很小时，泊松分布可作为二项分布的近似，其中为。通常当时，就可以用泊松公式近似得计算。同样也可以绘制一个示例来说明。

至此第八章的解题结束。