机器学习

机器学习练习笔记(九)

C-SVM：Cost-sensitive SVM，代价敏感SVM。

题目9.1 - C-SVM优化问题求解

线性神经元中存在一个未用在分类中的自由度。通过设置如下约束消除：

证明在此约束下，样本到决策边界上最近的一点被下式限制：

第二问，是写下C-SVM的拉格朗日的优化问题并解出C-SVM的对偶优化问题：

Missing or unrecognized delimiter for \left \underset{\lambda}{\max}\left{-\frac{1}{2}\sum_{\alpha=1}^{p}\sum_{\beta=1}{p}\lambda_\alpha \lambda_\beta y_T^{(\alpha)} y_T^{(\beta)} \left(x^{(\alpha)})\right)^T x^{(\beta)} + \sum_{\alpha=1}^{p}\lambda_\alpha \right}

其中：

关于SVM优化的证明过程及解释网上都有不少优秀的讲解，笔者在此就不展开了。

题目9.2 - 标准参数下的C-SVM

本题目是练习解决经典的“XOR”分类问题。首先通过前面章节题目7.1产生80个样本的训练集，然后通过同样的分布产生80个样本的测试集。这里不实现SVM算法，对于matlab，可以使用libsvm包；对于python则可以使用libsvm与scikit.learn；笔者使用的R中的e1071。

通过软件自身默认的C-SVM训练参数建立模型，并用将模型应用在测试集上。把决策边界显示出来，同时表示出支持向量。

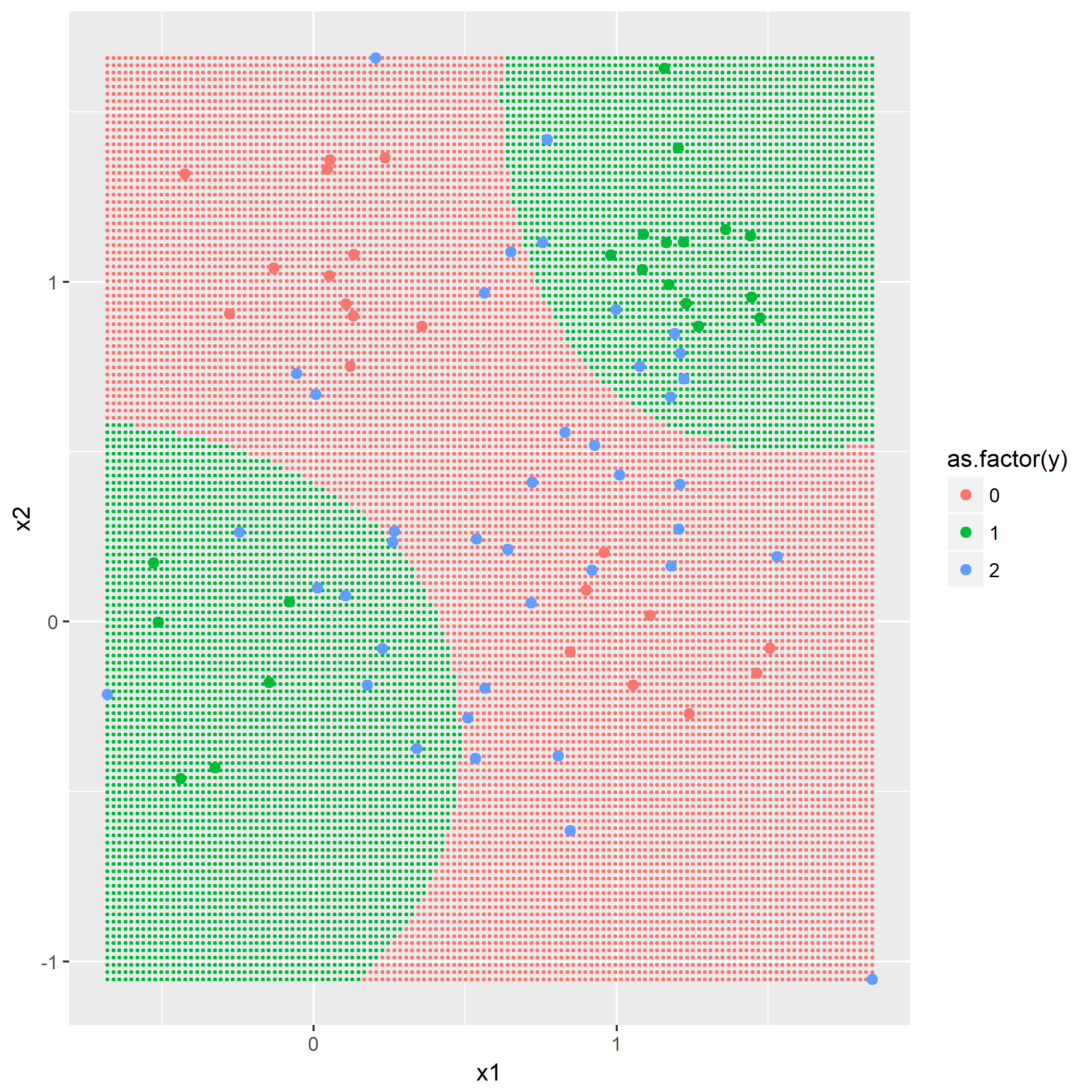
图中蓝点即为支持向量

题目9.3 - C-SVM参数优化

使用交叉验证以及网格搜索发找出C与核参数。使用指数增长搜索，如，画出交叉验证中训练集分类率，以及使用等高线画出参数空间下的关于这两个参数的值。

第二问使用上述所得的最佳，重做练习9.2。