逻辑斯谛回归模型

逻辑斯谛回归模型（Logistic Regression，以下简称LR）是统计学习中的经典分类方法。读过《统计学习方法》之后，笔者才知道该模型是一种概率分布模型，从此理解为何该模型不但可以预测分类，还可以预测属于该类的概率。

逻辑斯谛分布

设是连续随机变量，若服从逻辑斯谛分布，则有如下分布函数和密度函数：

下面两张是时的概率密度分布以及累计概率分布：

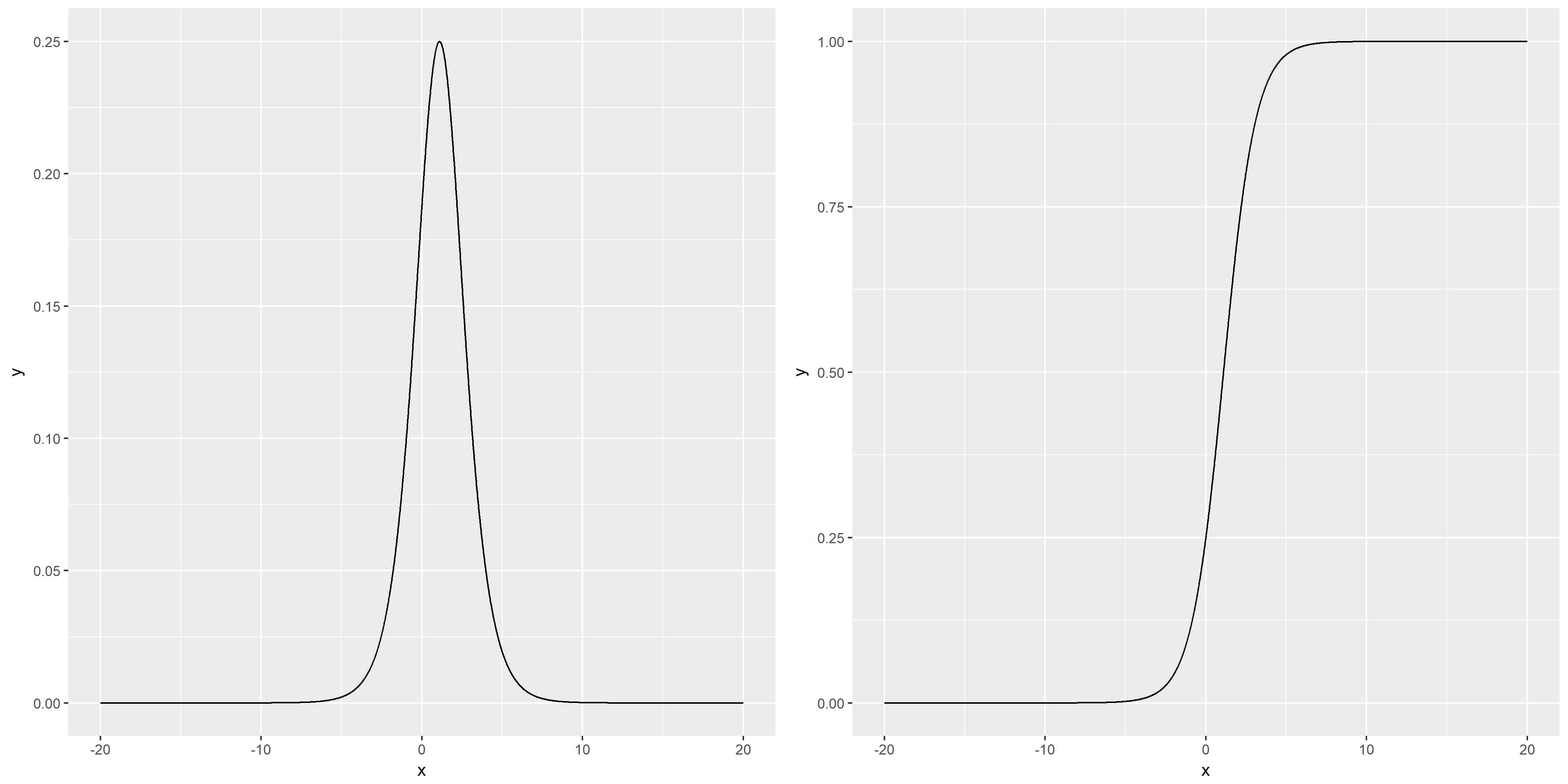
可以看到PDF关于Y轴对称，CDF关于对称。

曲线在中心附近增长速度较快，在两端增长速度较慢。形状参数越小，曲线在中心附近增长越快。

二项逻辑斯谛回归模型（Binomial Logistic Regression Model）是一种分类模型，由条件概率分布表示，随机变量取值0或1，。

故二项逻辑斯谛回归模型是如下的条件概率分布：

定义一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值。设事件发生的概率为，则该事件的几率是，事件的对数几率（logit odds）或logit函数：

将上述的代入到中，则有：

即，在逻辑斯谛回归模型中，输出的对数几率是输入的线性函数。

从另外一个角度看，考虑对输入进行分类的线性函数，其值域为实数域。此时，线性函数的值越接近于正无穷，概率值越接近1；线性函数的值越接近负无穷，概率值越接近0.

利用极大似然估计法可以估计模型的参数，设：

似然函数：

对数似然函数：

问题就转变为了以对数似然函数为目标函数的最优化问题。逻辑斯谛回归学习中通常采用梯度下降法或拟牛顿法。

对权重向量求偏导则可得：

采用，则偏导可以表示为：

这篇文章仅仅介绍逻辑斯谛回归模型，不介绍最优化常用的方法，读者可以寻找各类最优化方法，将上述提到的目标函数以及一阶偏导代入到各类优化方法中。