2018-06-21

工具使用

R配置Keras

TensorFlow基本上成为了深度学习的标配。但是为了学习主要的内容（忽略底层实现细节）或者快速实现一个神经网络模型，Keras是一个很好的选择。

Keras中文版文档

环境准备

安装步骤

安装R的Keras需要用到devtools::install_github()命令，因此需要安装devtools包。

但是笔者用的Windows 10，直接安装包不会报错，但是使用该包下的命令会出一些奇怪的错误，例如在装R-Keras时就报超时。

所以建议在Windows下使用该包时，先去安装Rtools。

同时需要安装好Anaconda，不然在后续步骤中会报错。

安装好Rtools之后，打开R命令行，在其中再安装一遍devtools包：

1	install.packages("devtools")

然后安装R的Keras接口：

1	devtools::install_github("rstudio/keras")

在命令行或者第一次运行Keras的脚本下输入：

1 2	library(keras) install_keras()

然后会调用Anaconda为R-Keras建立一个环境，成功初始化，在以后的R脚本就不需要再使用install_keras()命令了。

安装GPU支持

事实上这部分操作是属于Anaconda那边的操作，毕竟R-Keras用的还是Python的TensorFlow后端。

中文文档里面就已经很详细地介绍了如何准备GPU环境：

CUDA
cuDNN

文档写的时候上述Keras尚未支持高版本的CUDA和cuDNN，经笔者测试，是可以支持最新版的CUDA和cuDNN的。

安装好后，打开Anaconda Navigator管理软件，或者命令行模式：

1	$ activate r-tensorflow

切换到r-tensorflow环境，安装gpu版Keras：

1	$ conda install keras-gpu

等待安装过程（可能因为墙导致下载出问题，要么上梯子，要么辛苦一点重试几次安装命令吧）后，就可以开始使用了。

测试R-Keras

官网给了MNIST测试集作为Demo，然而AWS被墙了，整个Demo直接卡在下载数据集步骤就挂了。

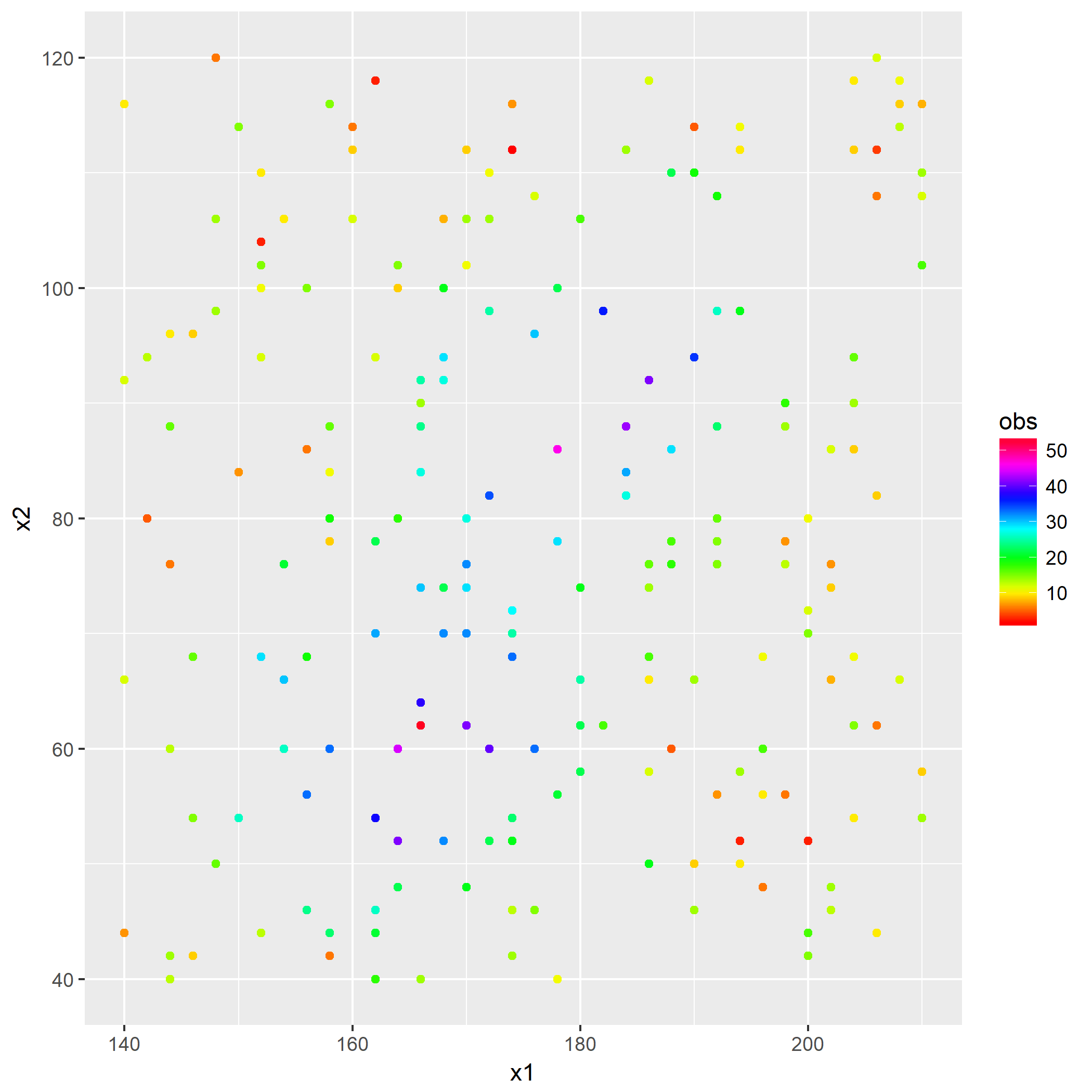
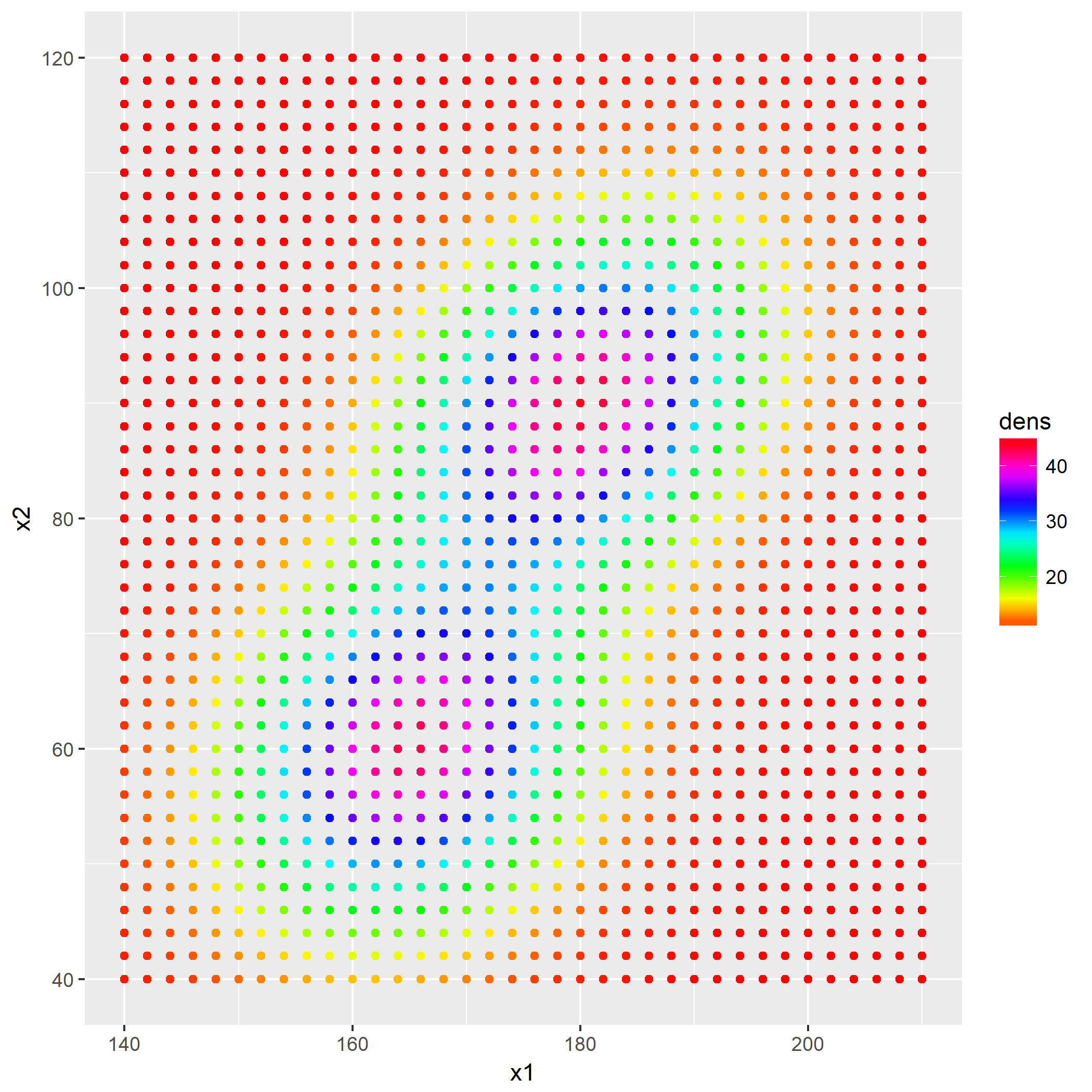
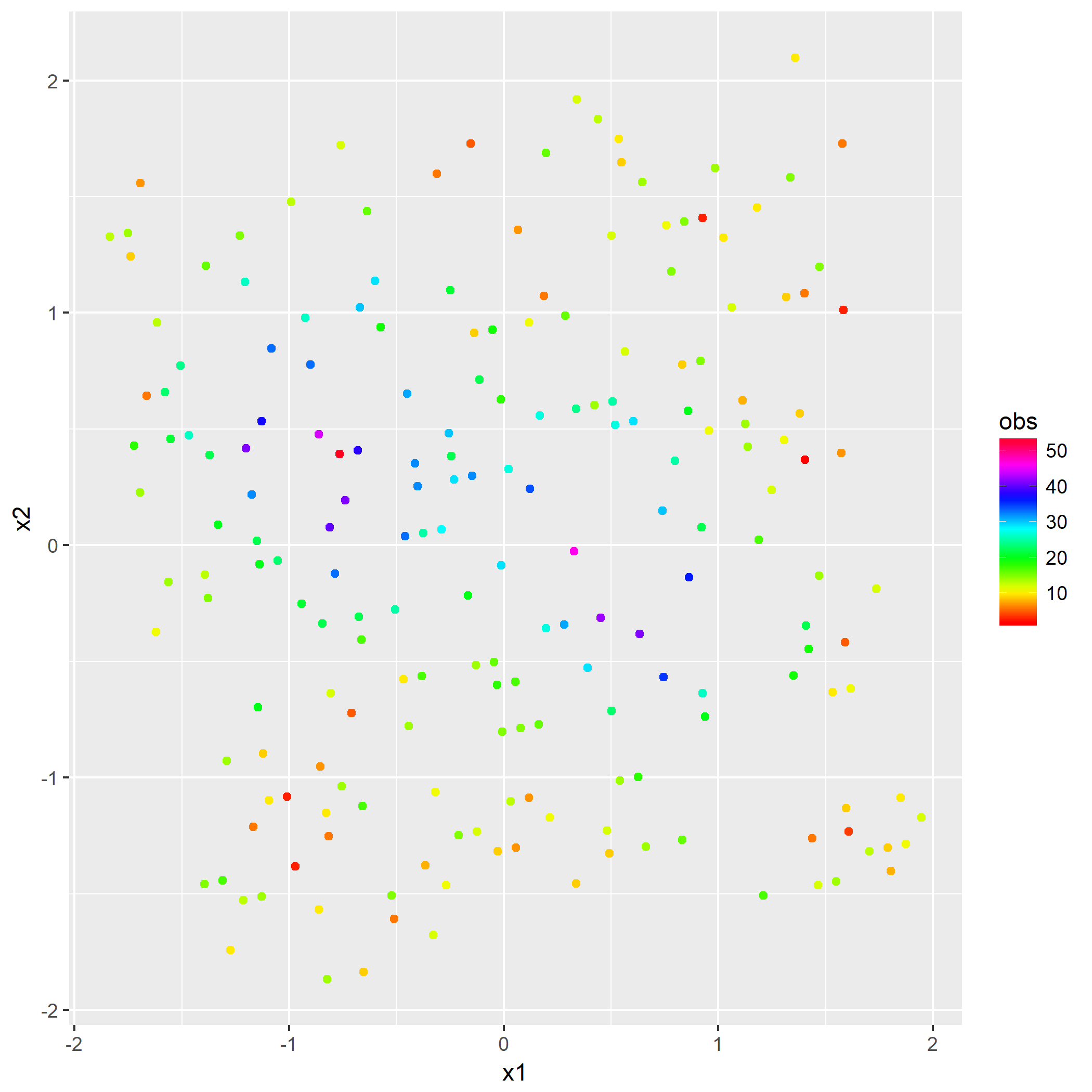
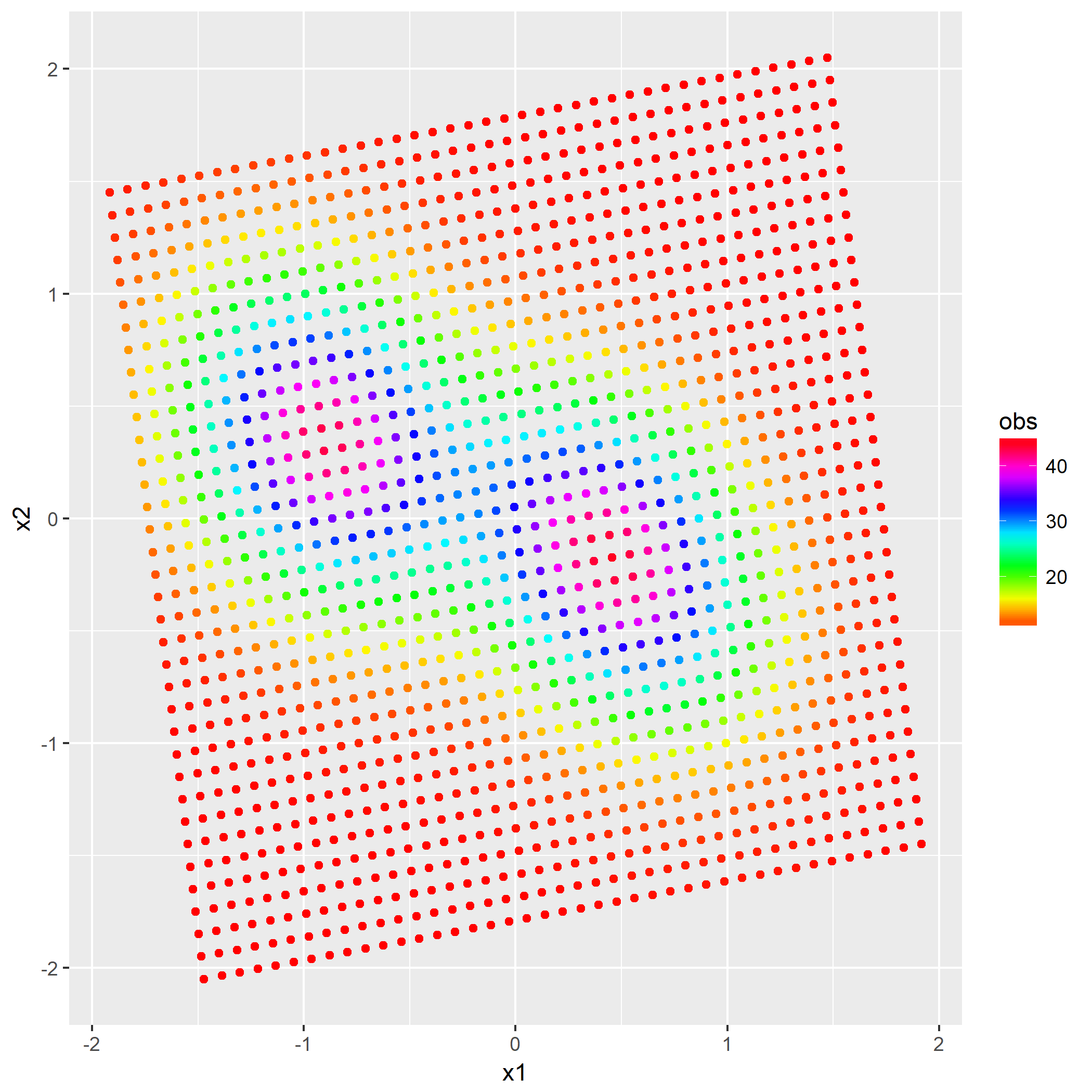
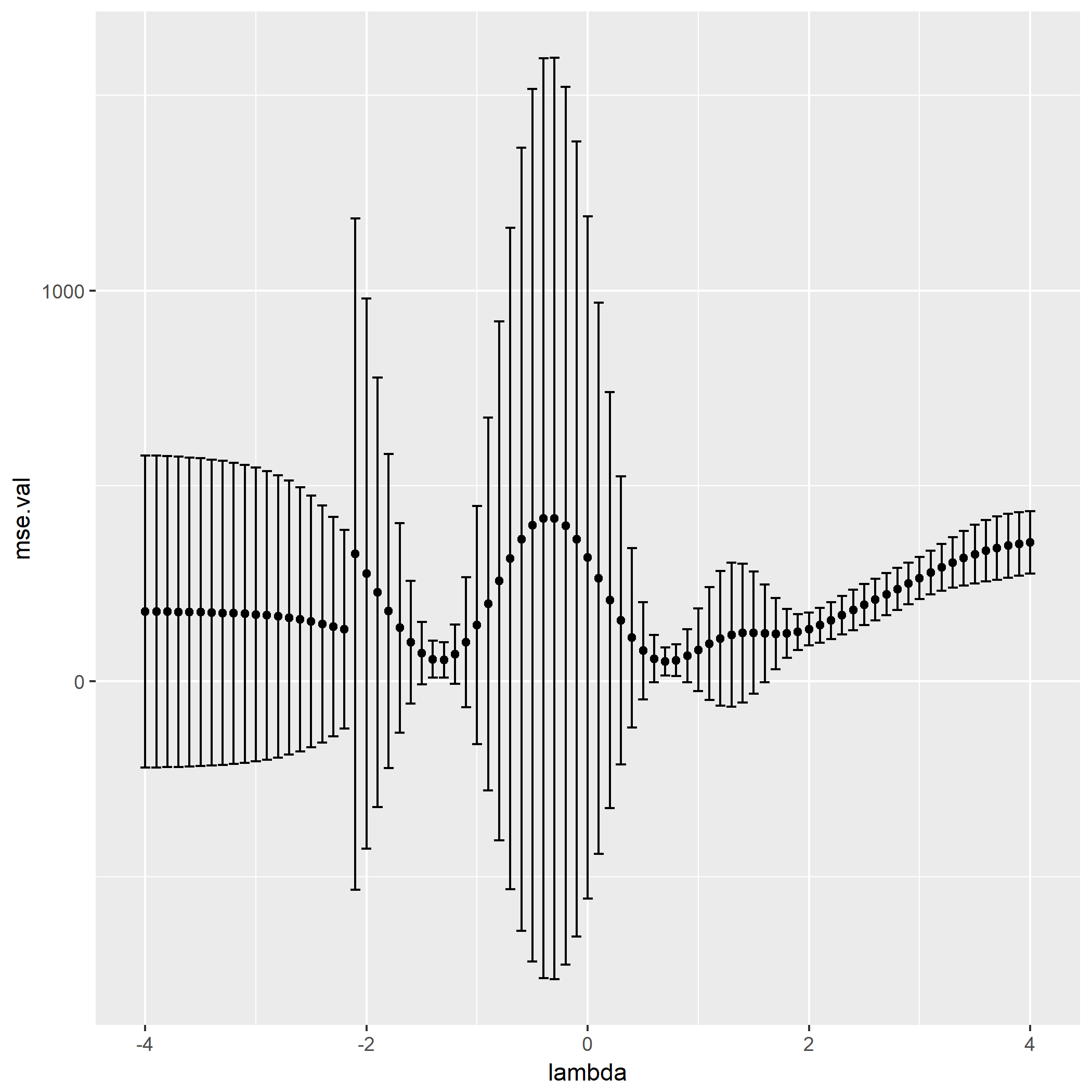
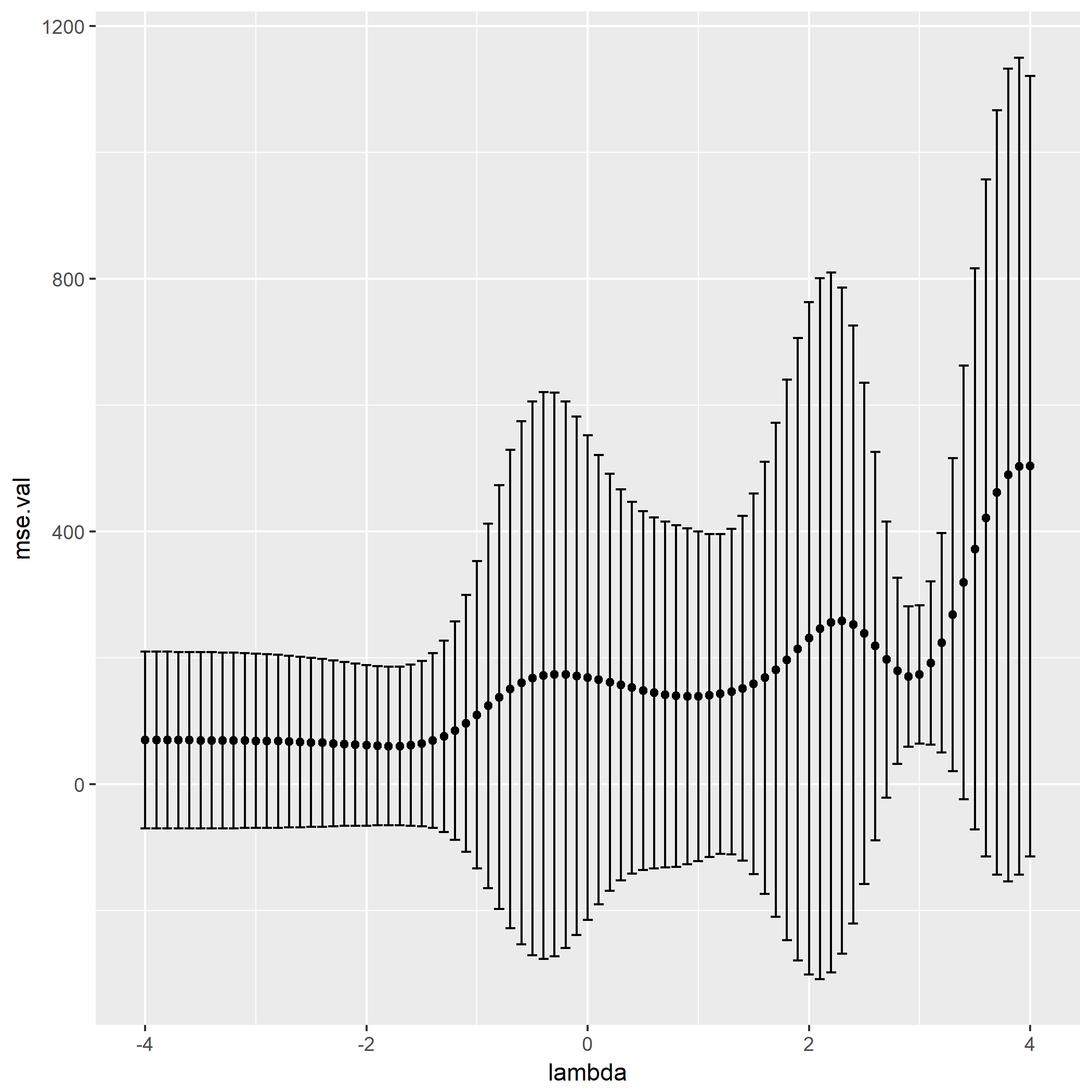
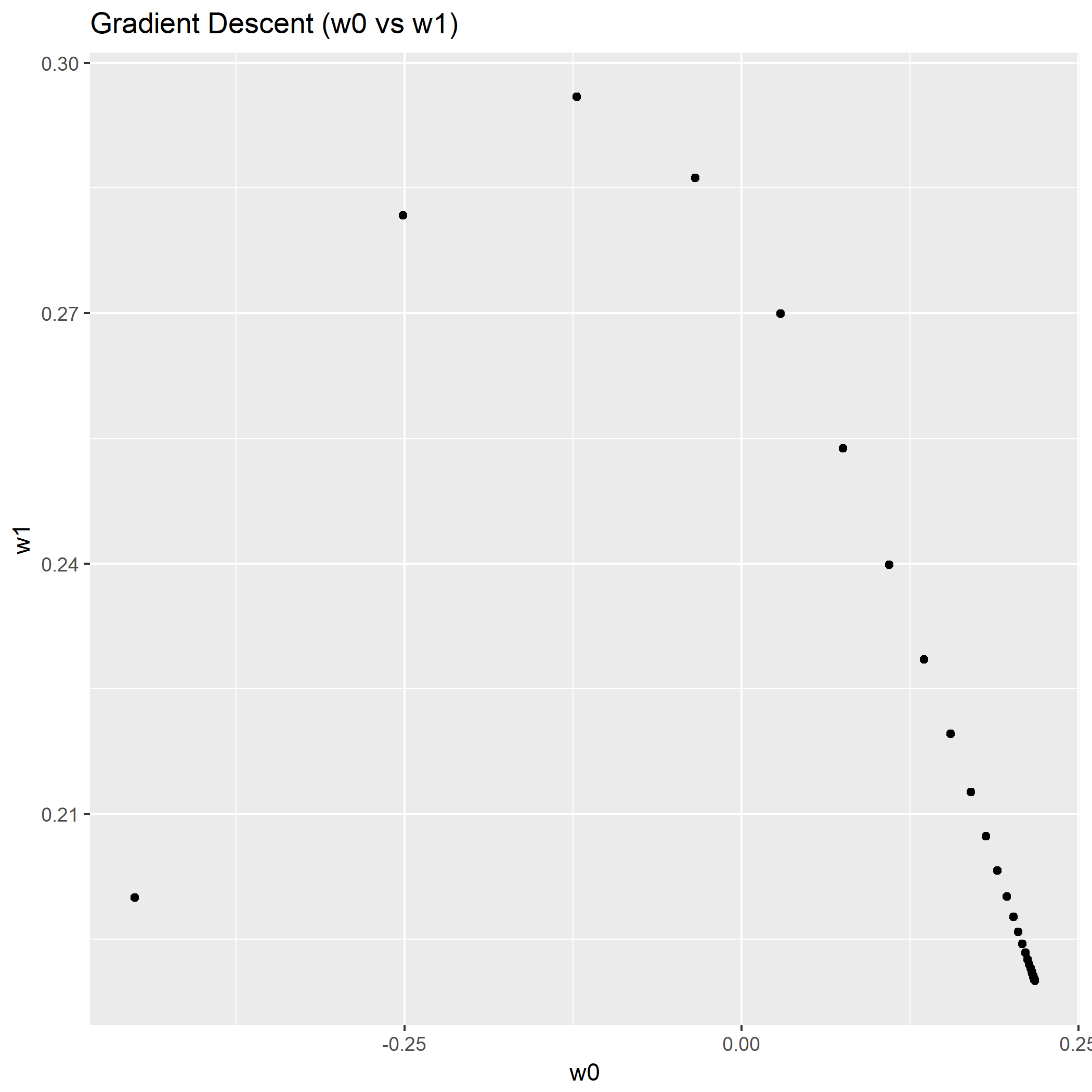
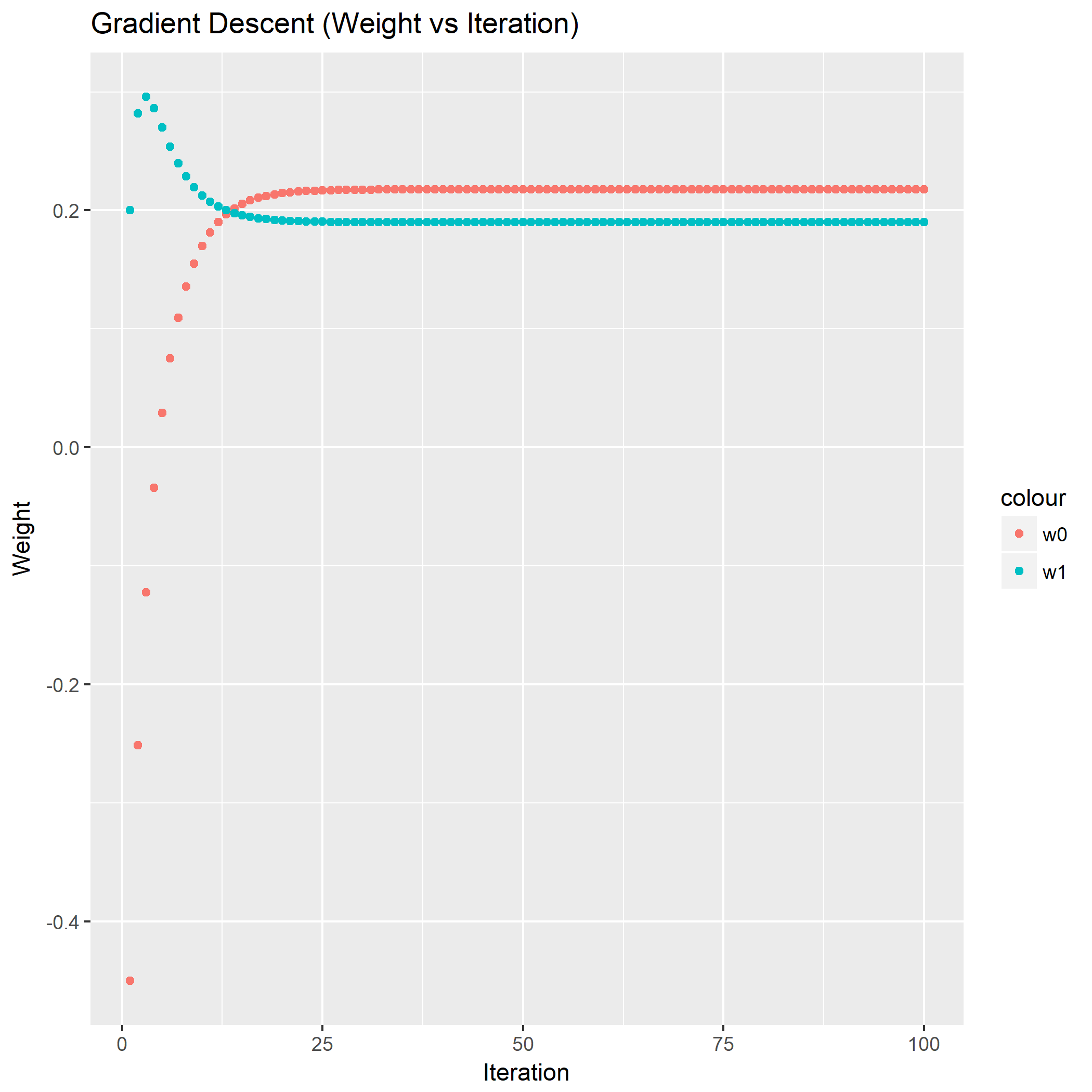
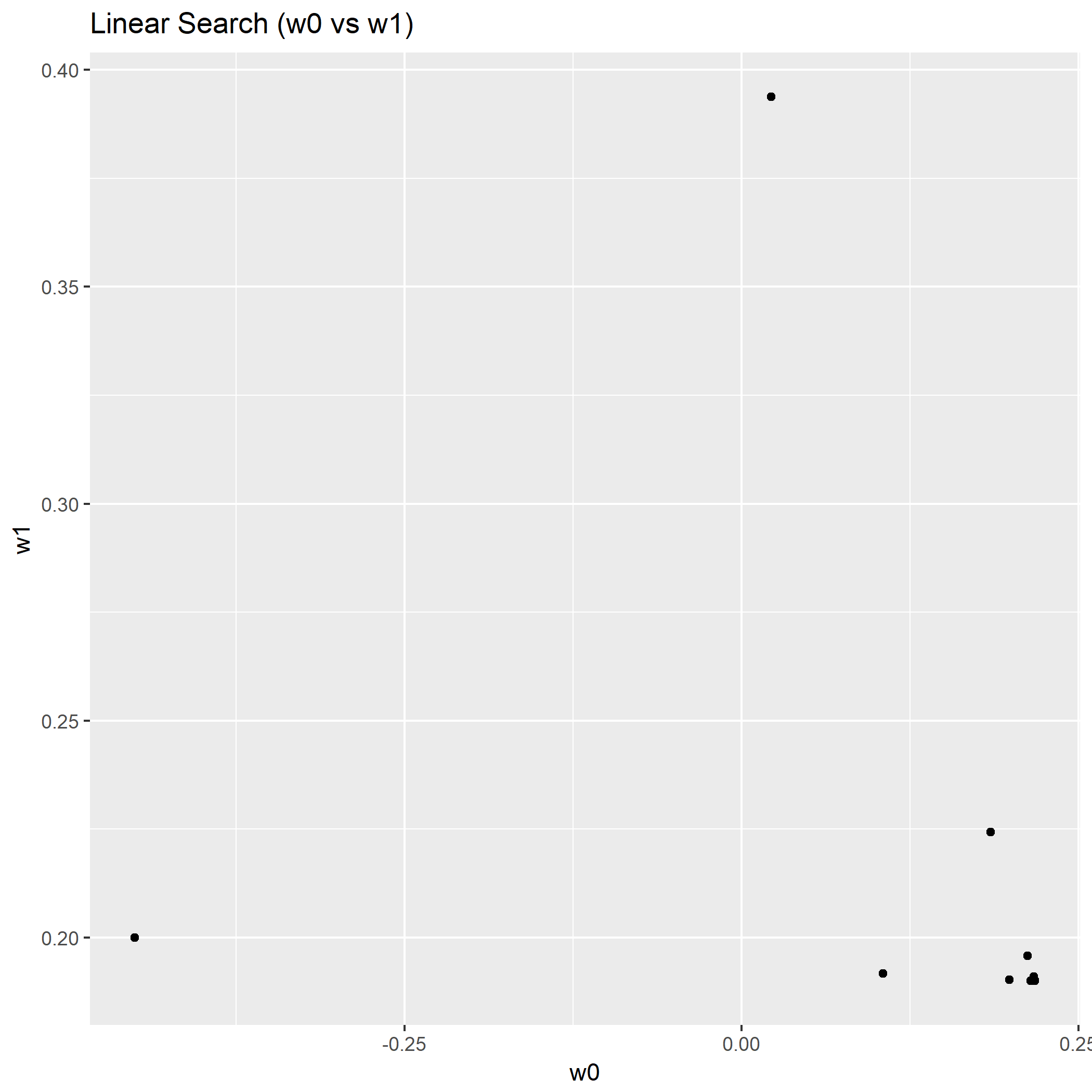
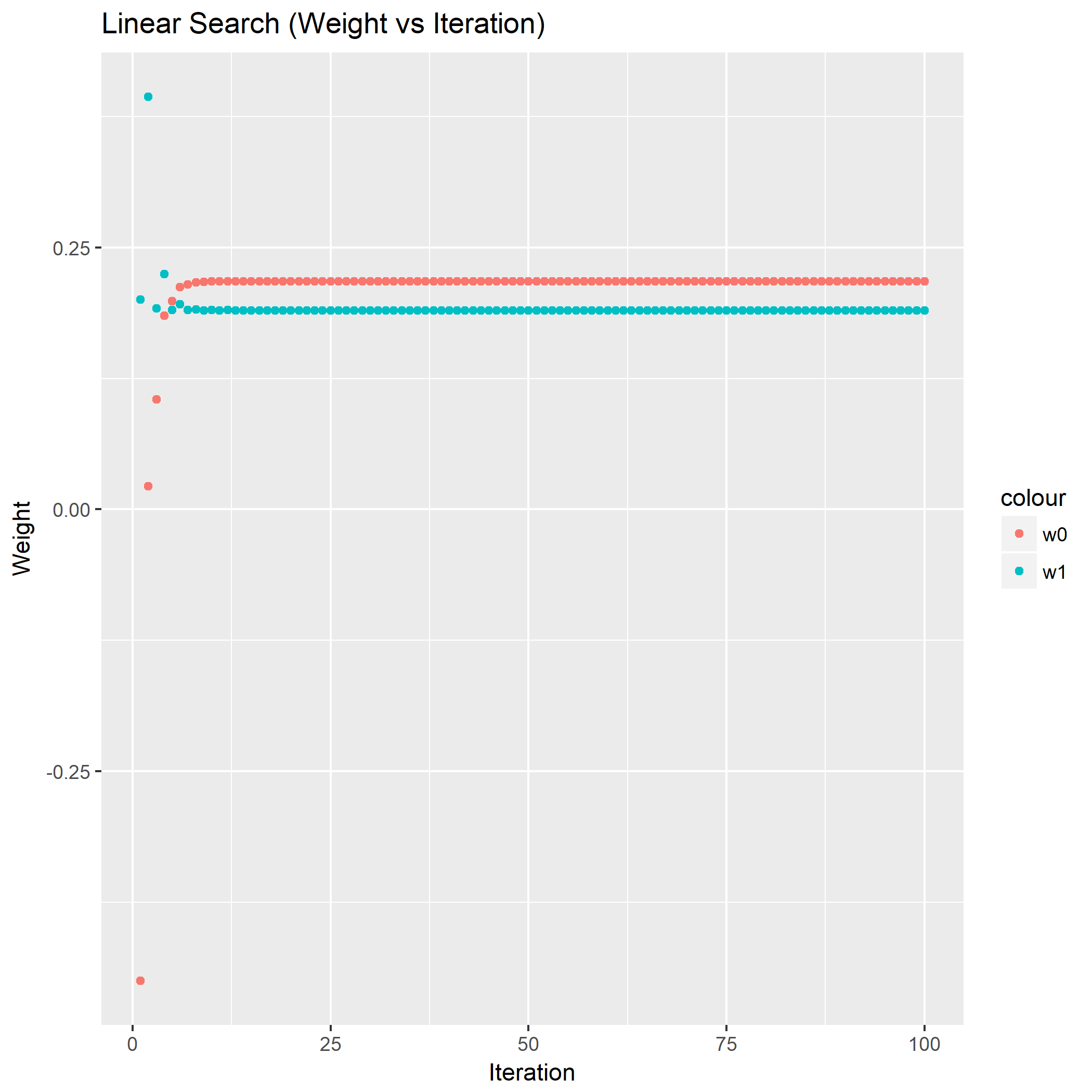
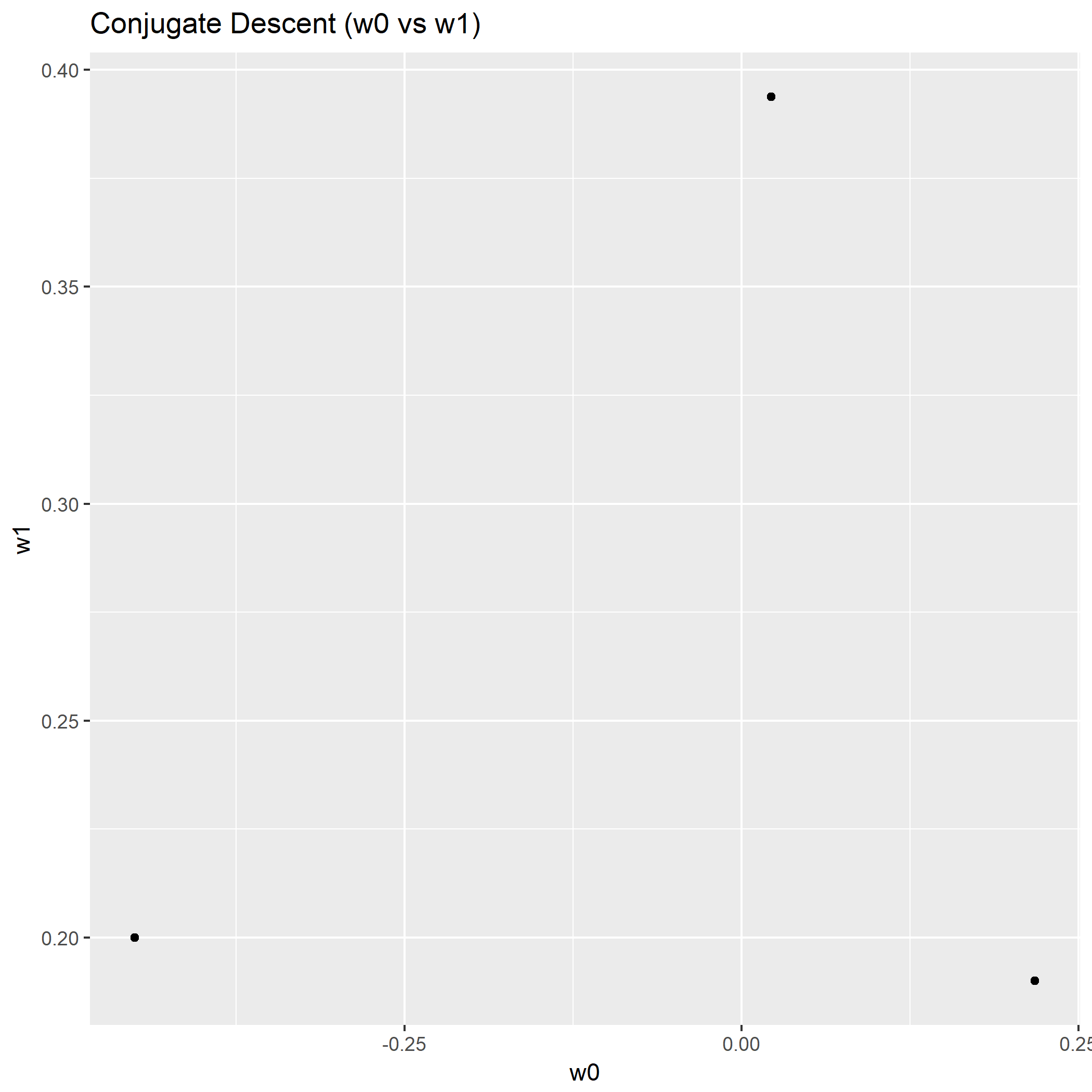
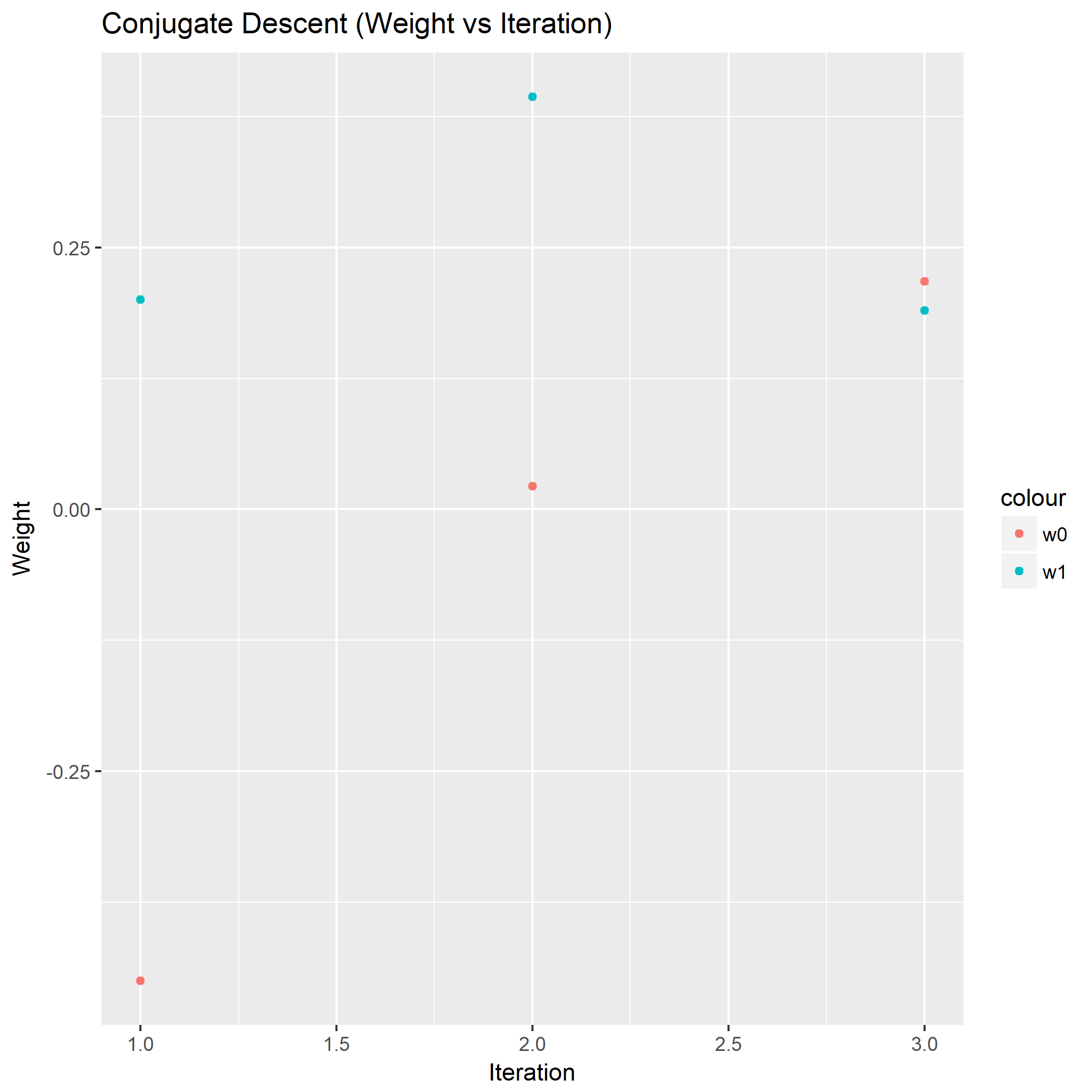
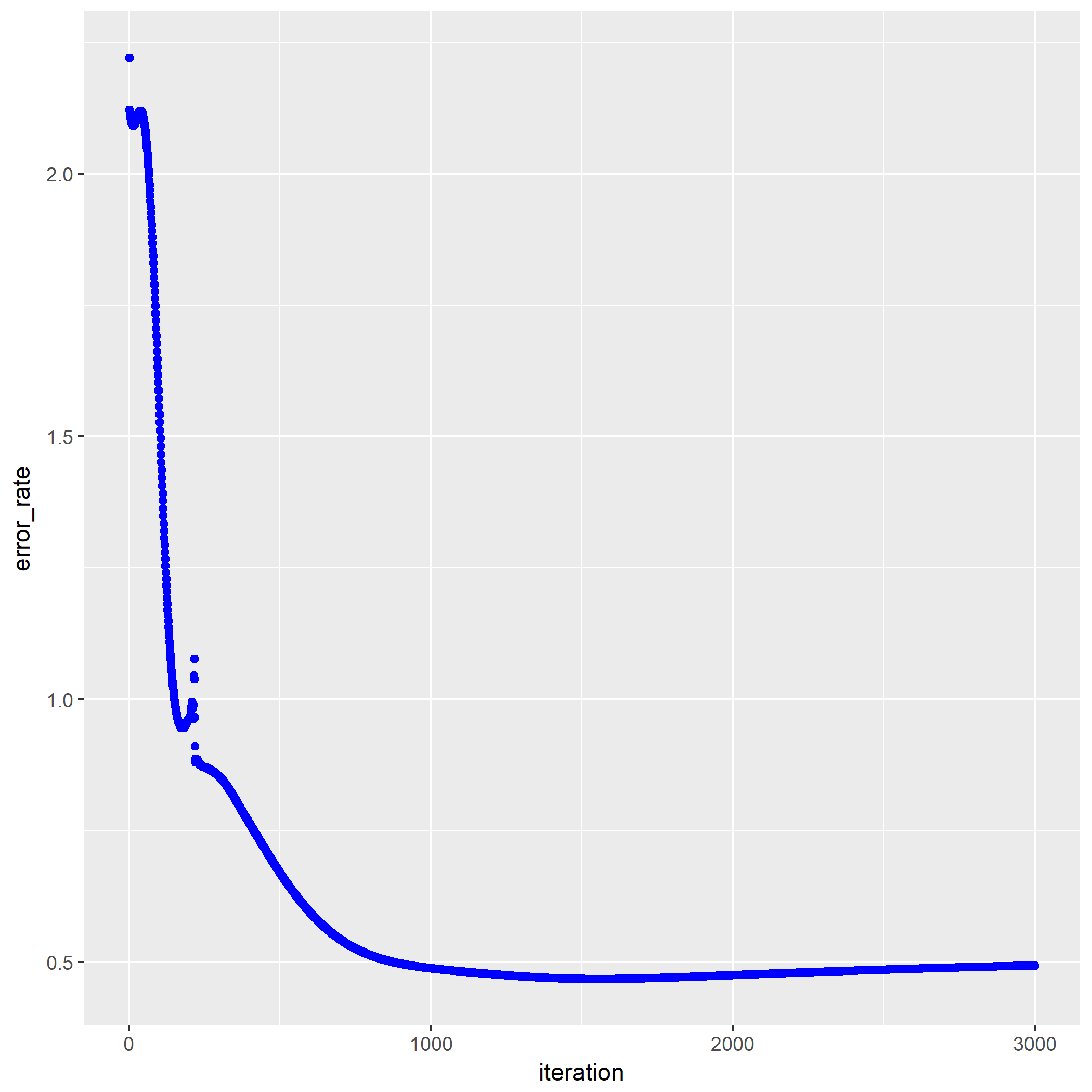
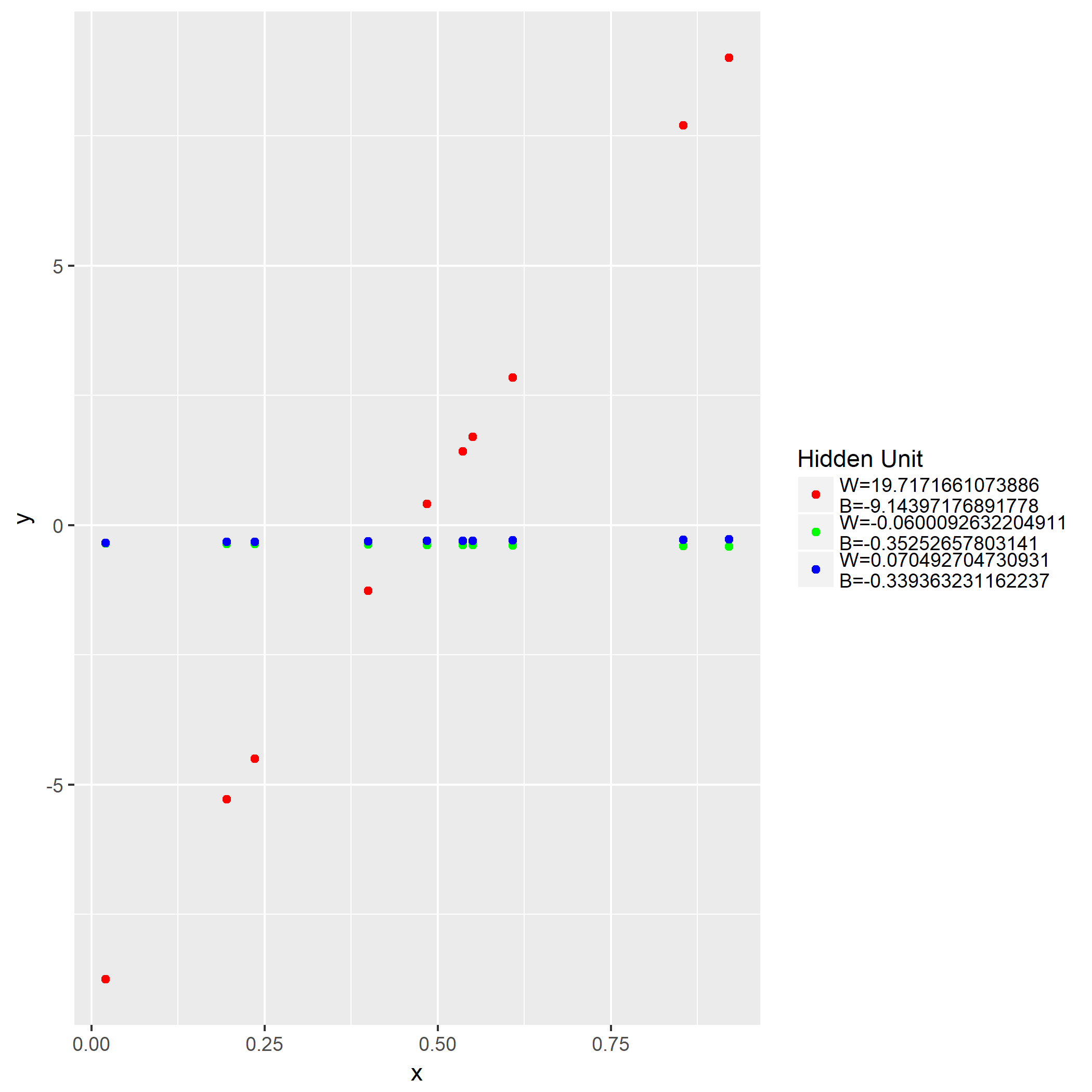
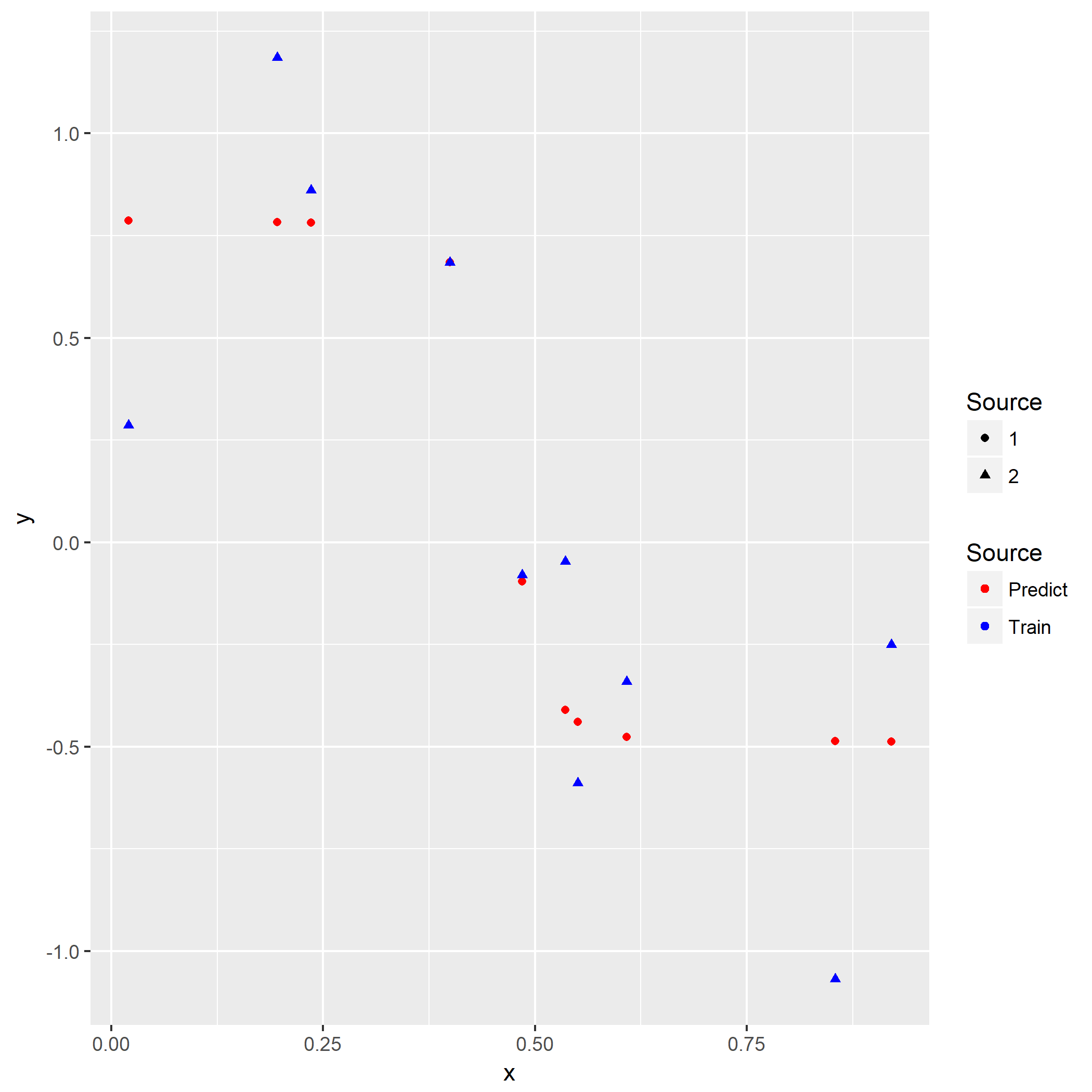
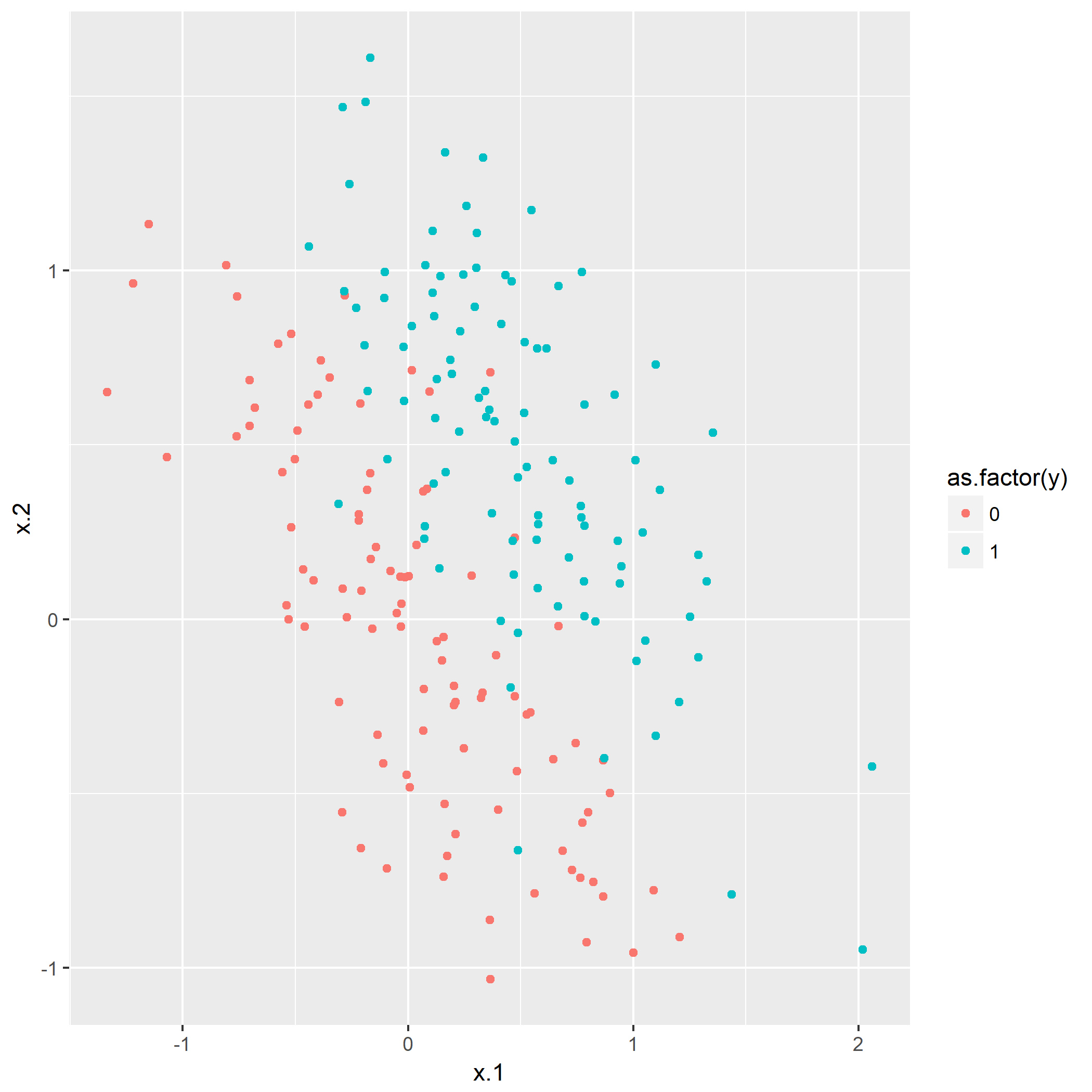
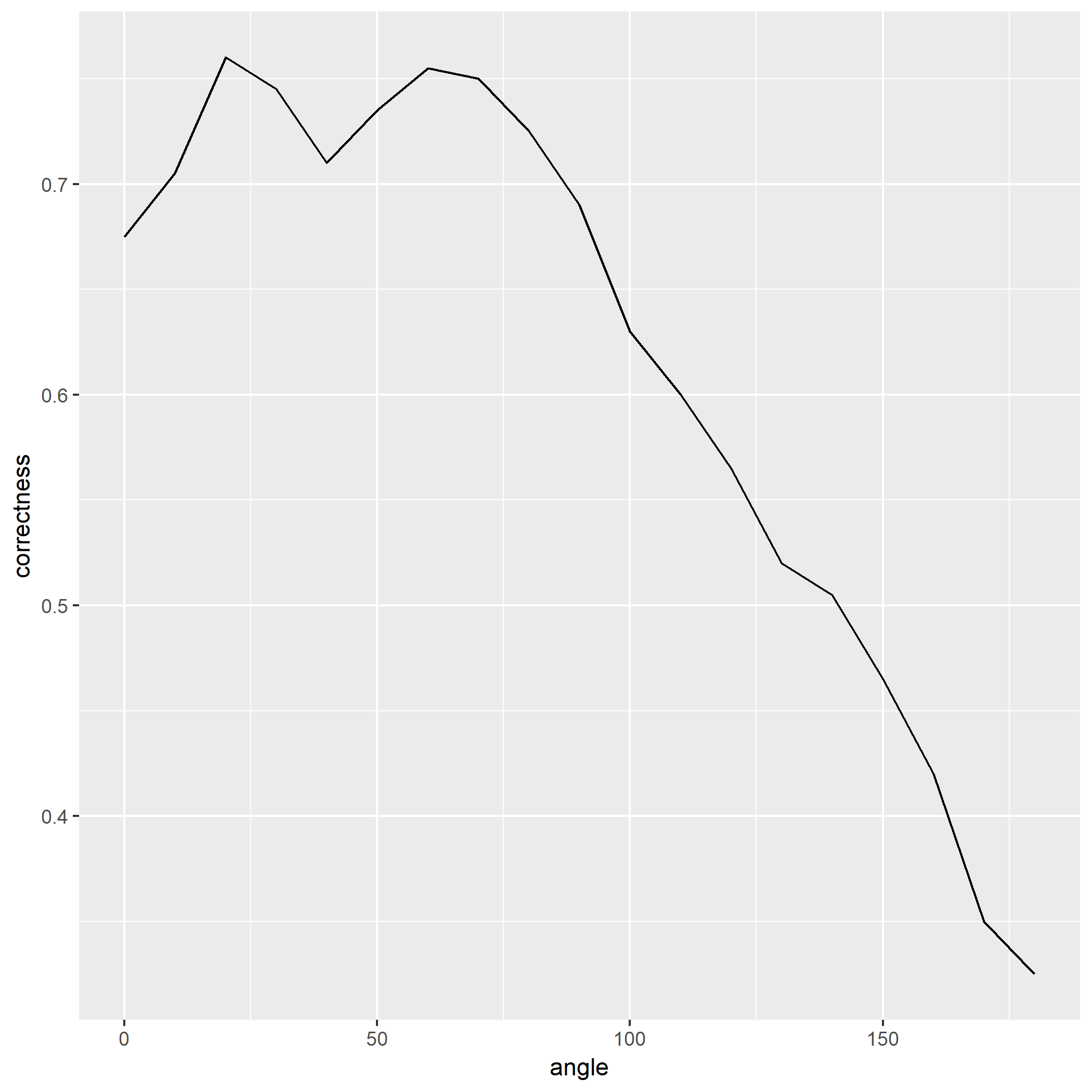
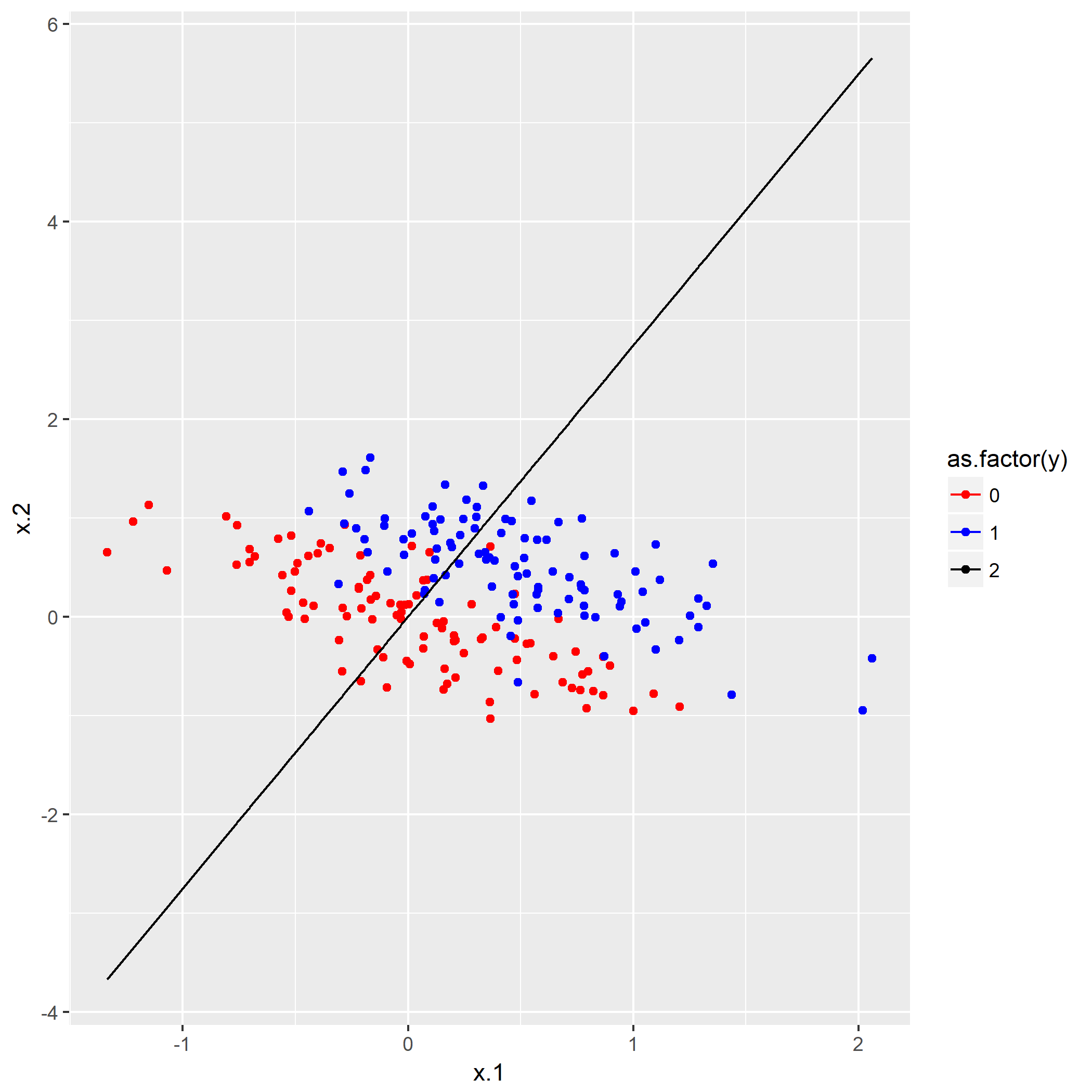
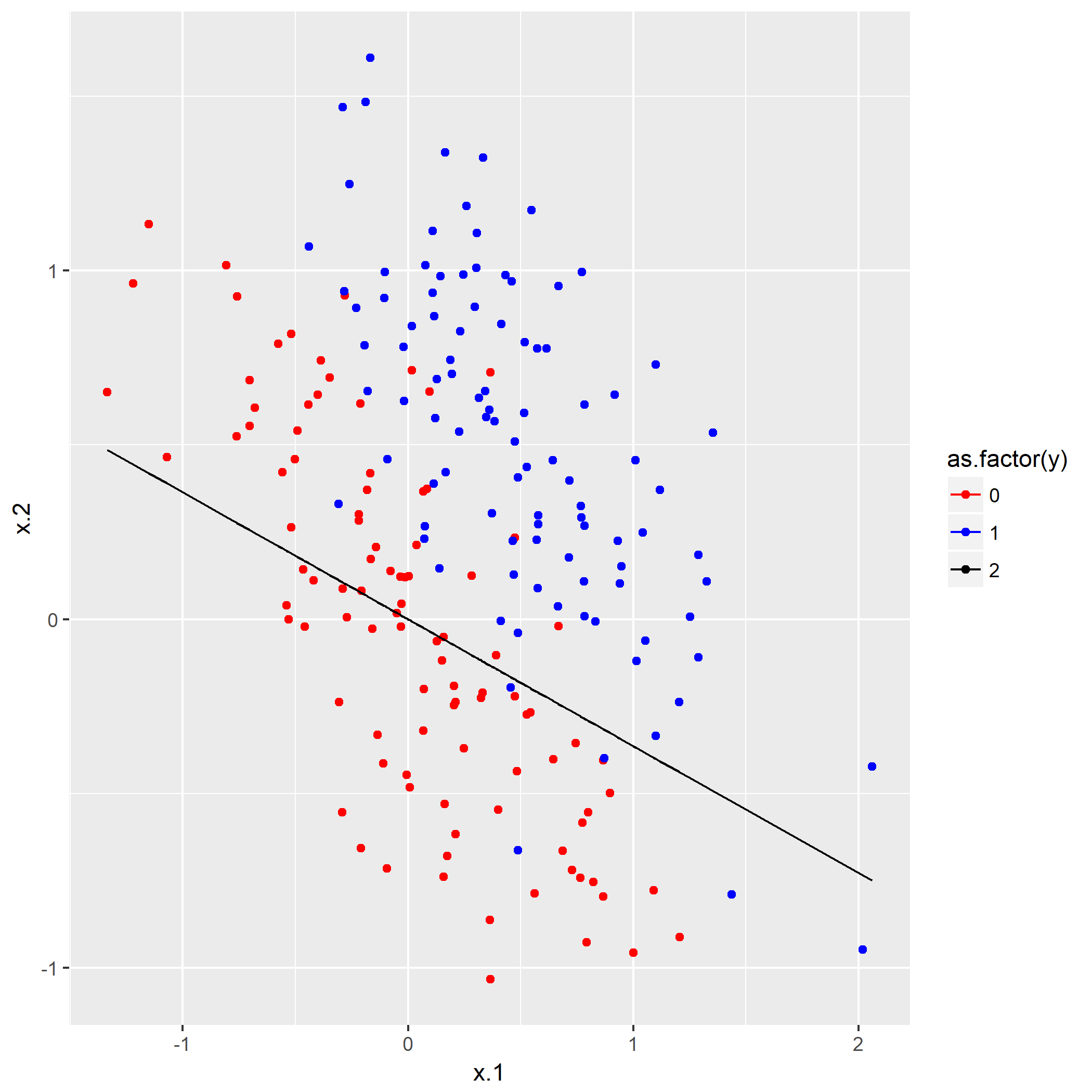
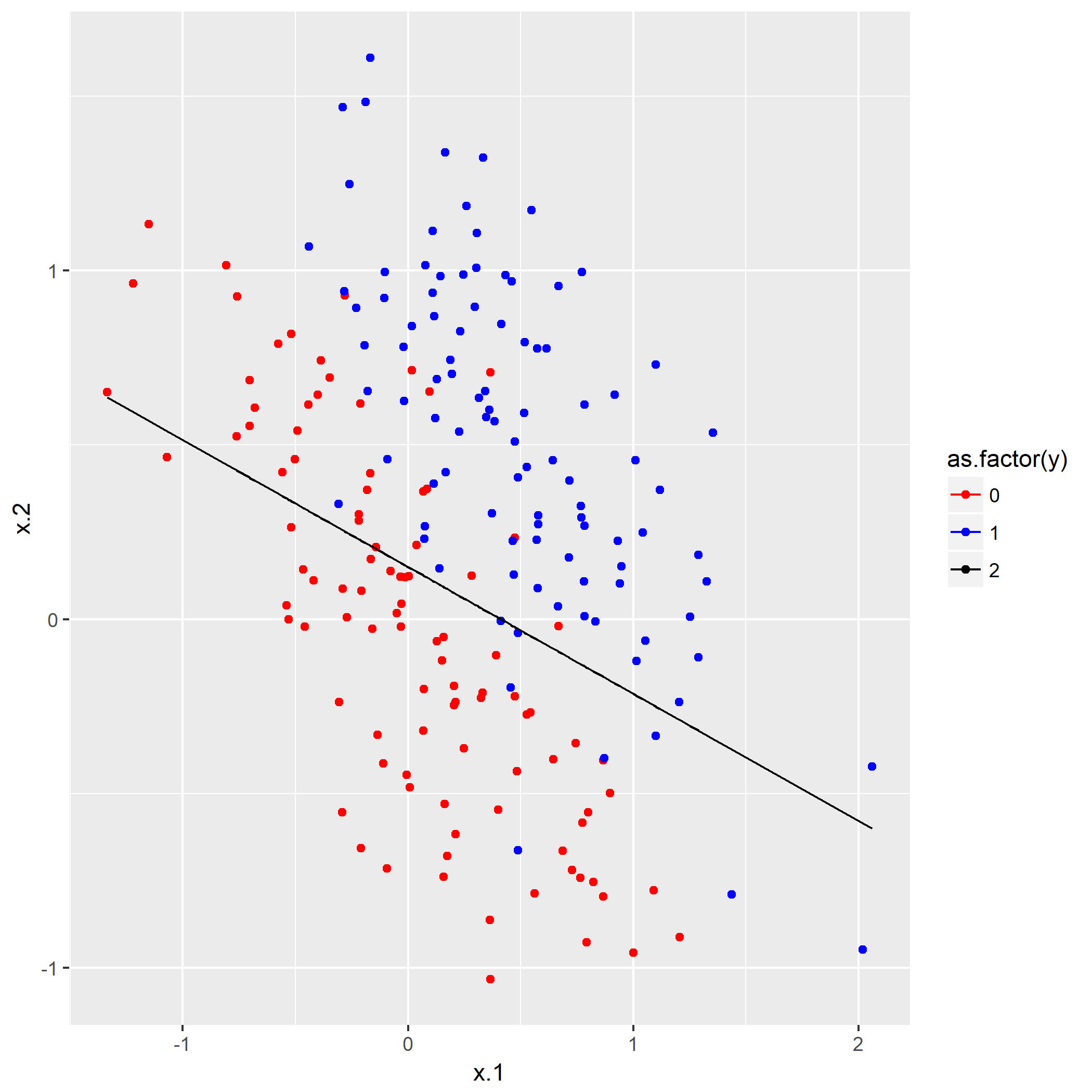
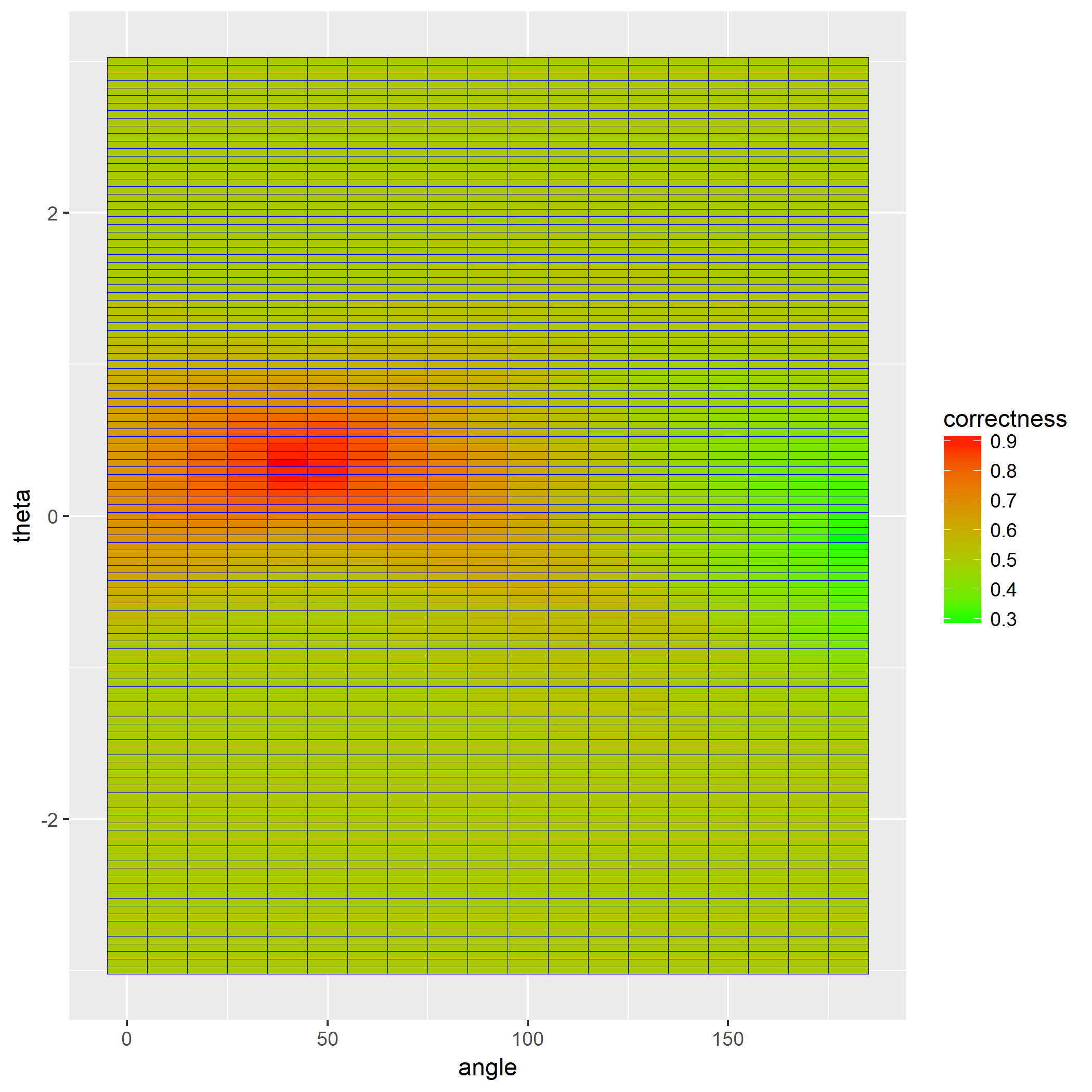
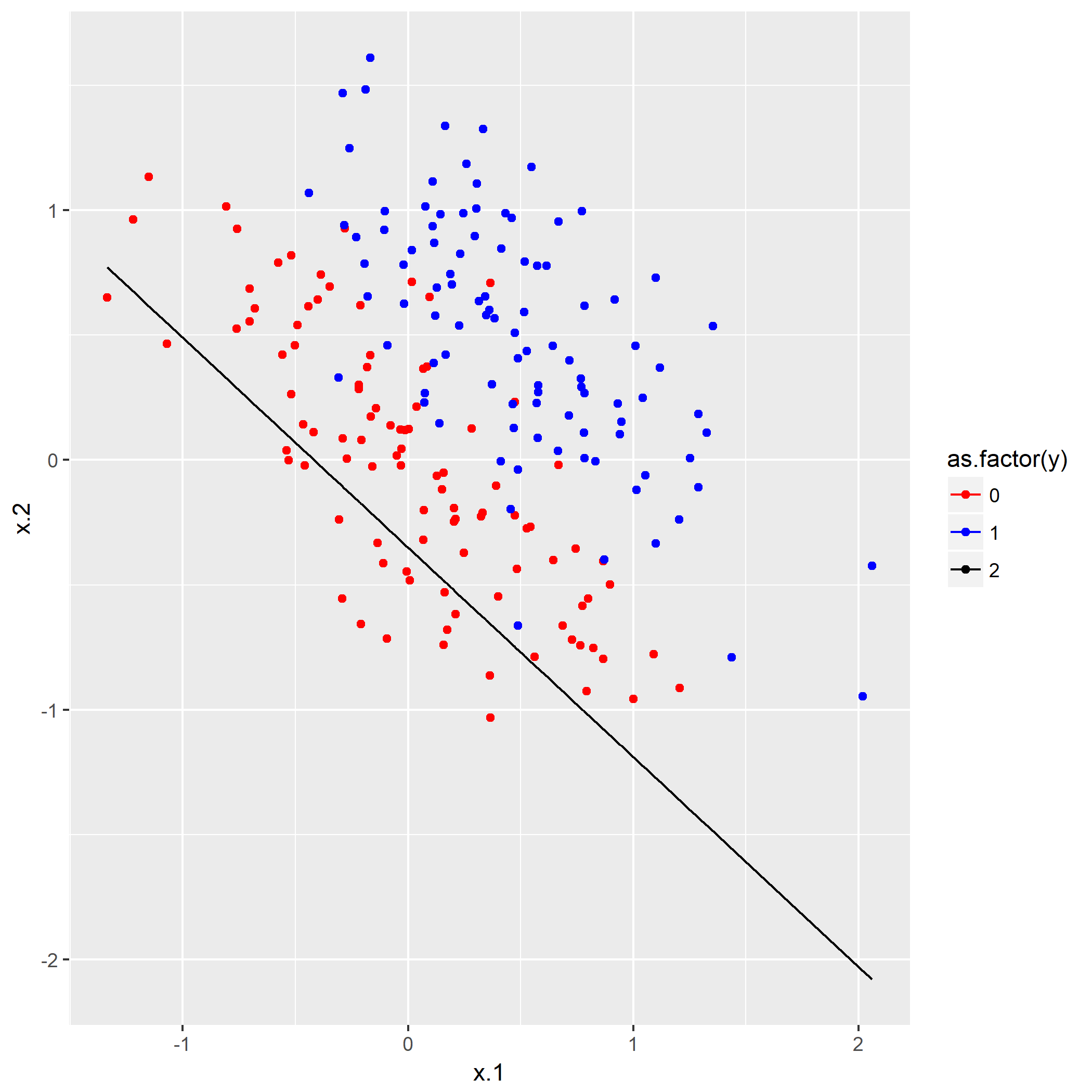
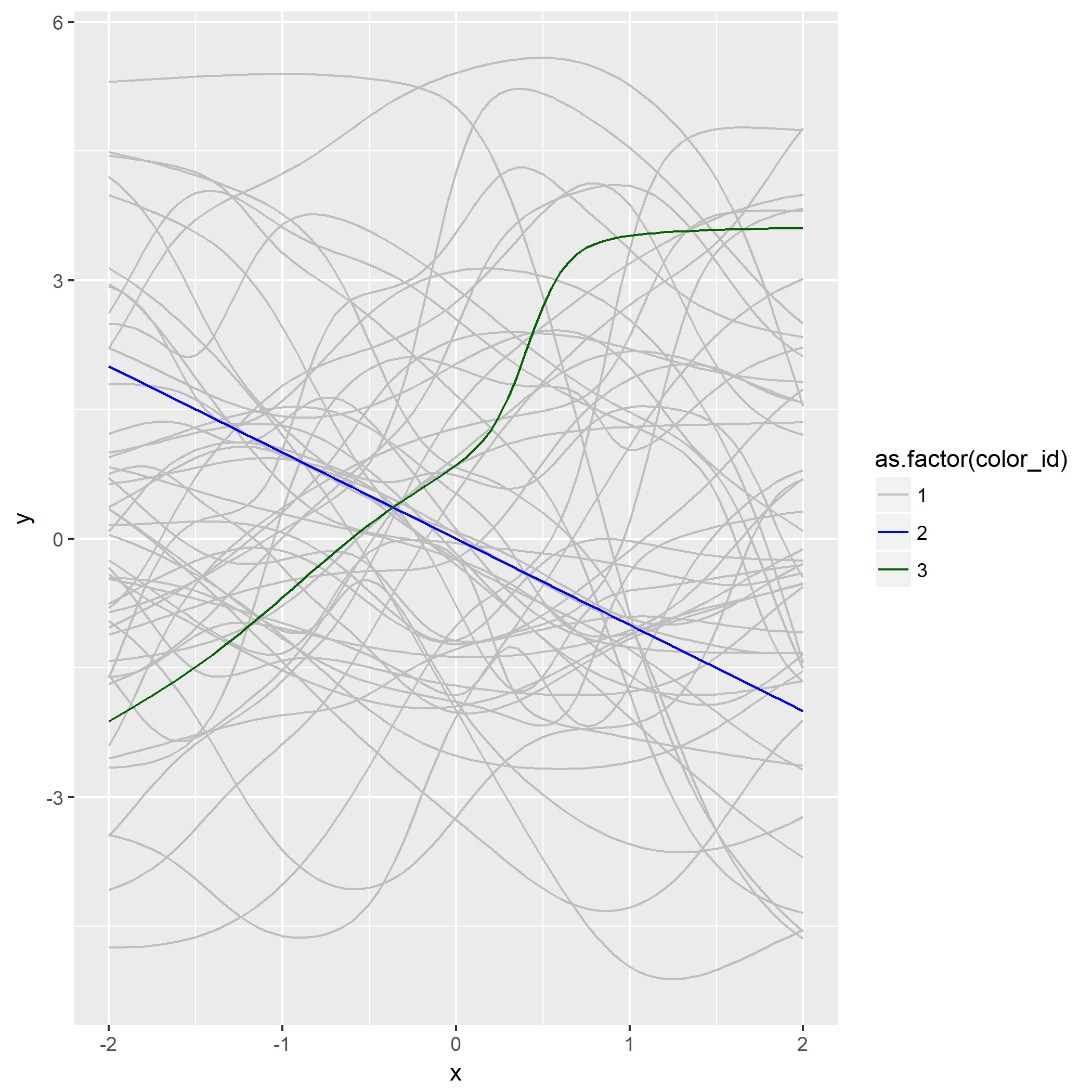
笔者写了个简单的脚本用于测试：

library(keras)
library(ggplot2)

script_dir <- dirname(sys.frame(1)$ofile)
setwd(script_dir)

# 产生sample.size * num_props的矩阵， 默认80%数据作为训练集，20%作为验证集
gensam <- function(sample.size = 10000, num_props = 30, val_portion = 0.2)
{
    all.x <- array(dim = c(sample.size, num_props))

    all.y <- array(dim = c(sample.size, 1))

    for(i in (1 : sample.size))
    {
        all.x[i, ] <- array(round(runif(num_props, 0, 9)))
        if(sum(all.x[i, ]) >= 100)
        {
            all.y[i, 1] <- 1
        }
        else
        {
            all.y[i, 1] <- 0
        }
    }

    split_point <- (1 - val_portion) * sample.size

    list(
        train = list(
            x = all.x[c(1 : split_point), ],
            y = all.y[c(1 : split_point)]
        ),
        test = list(
            x = all.x[c((split_point + 1) : sample.size), ],
            y = all.y[c((split_point + 1) : sample.size)]
        )
    )
}

# 产生一个数据集
dataset <- gensam()

# 准备训练一个LSTM网络，重塑数据集变成维度为(样本数量，序列长度，序列元素的长度)
x_train <- array_reshape(dataset$train$x, c(nrow(dataset$train$x), 30, 1))
y_train <- dataset$train$y

x_test <- array_reshape(dataset$test$x, c(nrow(dataset$test$x), 30, 1))
y_test <- dataset$test$y

model <- keras_model_sequential()

model %>%
    layer_lstm(units = 200, activation = "hard_sigmoid", input_shape = c(30, 1)) %>%
    layer_dense(units = 1, activation = "sigmoid")

# 编译模型
model %>% compile(
  loss = 'binary_crossentropy',
  # 使用ADAM优化
  optimizer = optimizer_adam(lr = 0.001, beta_1 = 0.001, beta_2 = 0.999, epsilon = 10e-8),
  metrics = c('accuracy')
)

# 训练模型并记录
history <- model %>% fit(
  x_train, y_train,
  epochs = 10, batch_size = 100
)

eval_report <- model %>% evaluate(
  x_test, y_test
)

# 输出训练完的模型在验证集的情况
print(eval_report)

plt.df <- data.frame(
  x = c(1:length(history$metrics$loss)),
  loss = history$metrics$loss,
  acc = history$metrics$acc
)

# 输出LOSS和ACC在迭代中的变化图形
ggplot(plt.df, aes(x = x)) + geom_point(aes(y = loss, color = "Loss")) + geom_point(aes(y = acc, color = "Acc")) + labs(color = "Type")

ggsave("history.png")

如果脚本成功运行的话，会在相同目录下产生一份名为history.png的图片，那么恭喜，安装成功了。

2018-05-27

机器学习

机器学习练习笔记(五)

该章里面涉及一个白化的概念。

在解本章题目之后，笔者认为除了算法实现之外的全部知识属于线性代数以及坐标变换，虽然题目要求与PCA算法有些不一样，但是其涉及到的线性代数知识是共享的，故理解白化过程之后，就很容易理解PCA了。

题目5.1 - 交叉验证

所用的训练集：

200个样本，其中。

以及验证集：

1476个样本，其中为坐落在图像的坐标信息。

第一问是将训练集以及验证集的数据白化后作图，首先画出白化前的数据分布：

白化前训练集

白化前验证集

在开始解题前已经介绍过白化过程了，于是直接贴出白化后的数据分布：

白化后训练集

白化后验证集

第二问是多项式展开，利用核函数将白化后的数据从2维升至更高维度，使得非线性问题在高维表示为线性问题。

所用的映射函数：

例如当时，可以产生55项这样的单项式，根据该映射函数，所用的预测方程为：

而。

然而本题要输出的是各单项式的值，例如当的时候，本题要求画出前10个单项式的值，这会产生10张图。

，即在前10个的组合中每对对应的值，绘图。

笔者懒得去画了，毕竟用ggplot将多张图片放在一个输出文件中有点麻烦，读者可以挑其中一个，如，以来绘出热度图。

第三问引入正则化来降低过拟合，这里用了L1正则化：

其中为单位矩阵，尝试不同的值对过拟合的影响，画出不同的平均方误差以及平均方误差的方差：

可以看到附近对于训练集正则化效果最好。

最后一问是试出对于验证集最好的，与比较一下：

然后最佳的，显然与不同。

至此第五章题解完毕。

2018-05-27

数学基础

线性代数-特征分解

特征值以及特征向量的定义

Wiki

科普材料

矩阵与维向量以及标量存在以下关系：

则称向量为矩阵的特征向量，为对应的特征值。

例如令，，则：

根据定义可以得到是的特征向量，而对应的特征值。

同时根据上述的定义，可得：

其中为单位阵。上述的结论可以用于求解特征值。

特征分解，谱分解 Eigendecomposition, Spectral Decomposition

Wiki

如果为实对称矩阵，则为正交矩阵，即，此时有：

应用1-矩阵幂的求解

假设方阵与有如下关系：

那么显然可以通过来求解方阵，而直接求解的话，反正笔者是摸不着头脑的了。

但是矩阵分解后的特征值对角阵拥有良好的性质，对对角阵施加幂运算，可以直接对对角线元素直接做幂运算即可：

奇异值分解， Singular Value Decomposition

特征值分解只能针对方阵，因而对于一般的矩阵，更加实用的方法是SVD。

Wiki

在实数域下，，其中方阵是对作特征分解得来的特征向量组成的矩阵，而是对作特征分解的来的特征向量，矩阵则是特征值矩阵。

2018-05-06

机器学习

机器学习练习笔记(四)

题目4.1 - 线性搜索

考察一般梯度下降用的更新公式：

第一问是用2阶泰勒对任意在的近似展开。

泰勒展开定义式

于是根据定义式有：

第二问是利用上述推导式以及不等式推导步长的上下界。

$$
\begin{align}
E^T(w_{t+1}) & \leq E^T(w_t) \
E^T(w_t) - \eta_t d_t \nabla E^T(w_t) + \eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq E^T(w_t) \

\eta_t d_t \nabla E^T(w_t) + \eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq 0 \
\eta_t^2 d_t^T \mathbf{H} E^T(w_t) d_t & \leq \eta_t d_t \nabla E^T(w_t)
\end{align}
$$

不等式至此需要分情况讨论了。

当时，有且仅有；

令符号，则有：

当或时，；

当时，为大于零任意值。

第三问通过求解当前权值下最优步长。

首先查看二阶泰勒展开式：

根据链式法则有：

而：

可得：

另外：

所以：

令算式等于0即可解得的表达式。

最后一问是证步长与搜索方向正交，这题笔者真不会证了。

题目4.2 - 下降方法比较

该题比较三种下降法：

学习率为常数的最速下降法
线性搜索学习率的最速下降法
共轭梯度法

题目细节以及算法描述，笔者不再赘述。

利用公式，画出常数学习率的最速下降法权重分布图以及关于迭代变化的图：

利用线性搜索的最速下降法：

显然可以看到用了线性搜索步长的最速下降法收敛速度提升很明显，从权重分布图来看不少的点集中在的最优解附近，从关于迭代的图来看，收敛到最优解的迭代次数要少些。

剩下的共轭梯度法：

虽然设定了最大迭代次数为100，然而共轭梯度法收敛到最优解之后，就不会产生合法的更新值了，所以第三轮迭代以后算不出步长，只能强制在收敛时结束迭代。

由此对比，共轭梯度法取得了最好的表现。

至此，第四节的问题解决。

2018-04-27

数学基础

拟合优度检验入门

置信度与显著性水平

注意点

由AD公式或KS公式所得的出的统计量（AD检验值为z，KS检验值为D_n），注意这里z服从的并不是标准正态分布，故不能用z-test来求得z对应的P-Value。而AD公式得出的z值服从的是其论文提及的，一个异常复杂的分布公式。

在说明z服从何种分布前，均不能使用任何公式对其求对应的p值。假设z服从正态分布，那可以用正态分布的累积密度函数求得z对应的P-Value；若服从帕累托分布，则可以用对应的累积密度函数求其p值，等等。

要注意的是，进来的样本数据求出来的z值已经不与原来的样本数据属于同一种分布了，也不是同一个概念了，故不能使用样本数据的零假设对应的累积密度函数来计算这个z值对应的P-Value（这是用来针对样本数据计算的）。应查清楚在该种分布下使用AD公式得出的z值用AD的P-Value计算式，或用其近似表达式求得，D’Angostino写出的书给出了大部分的近似表达式。

2018-04-21

工具使用

Win10下gem报SSL错误的解决方案

问题现象

最近在Win 10电脑上装了Ruby的环境，因为在VS Code有关的插件要用一些依赖，在gem执行安装命令的时候总报错误：

不推荐的解决方案

经过搜索求助，发现并没有有效的解决方法，根据Ruby China的解决方法，实在不行可以将~/.gemrc中的设置改为：

1
2
3

:sources:
- http://gems.ruby-china.org
:ssl_verify_mode: 0

注意要将https换为http，设置:ssl_verify_mode: 0关闭SSL功能。

但是这样就没有了安全性了，对安全有要求的看官估计也不太接受这个解决方案。

原因发现及解决方案

若是曾经安装过Ruby的用户，那么该解决方案应该很有参考价值。

Ruby China上也说了，如果配置正确的话是不会发生SSL错误的，加上笔者最终在网上搜索到一个近似的案例以及解决方案。

最终在电脑的环境设置中找到了SSL_CERT_FILE选项：

笔者猜测是装旧版本时安装器就设置了这个环境变量，而卸载时这个变量并未随之被取消，新版本安装器探测到了已经设置该变量就不再检测并更正了，导致了笔者后面几次安装Ruby之后都无法正常使用gem。

安装的Ruby 2.4.1里面SSL证书的路径为：

1	C:\Ruby24-x64\ssl\cert.pem

基本上就可以确认是变量的不正确设置引起的，更正变量为：

启动命令行并执行一些gem命令：

命令正常运行，问题解决。

2018-04-16

机器学习

机器学习练习笔记(三)

题目3.1 - 误差逆向传播公式推导

设为训练集的输出，为网络的输出，误差函数：

其中：

第一问求证：

这些符号里面的上下标太让人眼花了，笔者首先用其他符号代表一下：

那么条件就变成了：

问题就变成了：

开始求解：

证之。

第二问，有如下函数：

其中为第一层到第二层的总输入，求证：

这个求导基本上就是在考本科学过的求导知识,同样先简化符号：

证之。

结合前两问，证明：

其中是第一层（隐藏层）的第个神经元到第二层（输出层）的第一个神经元的权重，是第一层的第个神经元的输出。

这里的符号一样混乱，但是在简化符号代表之前首先展开并理清：

因为机器学习里面的一般方法就是设定一个误差函数，然后使得误差函数最小化，其中一个重要的方法就是求导，通过导数找到极小值点。

理解这样的展开技巧是很有必要的，因为这里是一层（隐藏层到输出层）的求导，稍后误差函数关于输入层的权重的偏导数也要进行类似的展开。

根据上式以及第一问求得的，简化表示。

而函数为第二问提及的函数，利用结论可得：

简化表示为：

剩下的

注意到：

其中为隐藏层的神经元个数。

故可以求得：

所以：

证之。

题目3.2 - MLP回归

首先先观察MLP的结构：

在前面一题得到了隐藏层的权重更新公式：

在开始求解问题之前，需要得知输入层的更新公式，仿照上一题的推导过程，有：

$$
\begin{align}
\frac{\partial e^{(\alpha)}}{\partial w_{ji}^{10}} & = \frac{\partial e^{(\alpha)}}{\partial y(x^{(\alpha)}; w)} \frac{\partial y(x^{(\alpha)}; w)}{\partial h_1^2} \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = \frac{y(x^{(\alpha)}; w) - y_T^{(\alpha)}}{y(x^{(\alpha)}; w)(1 - y(x^{(\alpha)}; w))} y(x^{(\alpha)}; w)(1-y(x^{(\alpha)}; w)) \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] \frac{\partial h_1^2}{\partial S_j^1} \frac{\partial S_j^1}{\partial h_j^1} \frac{\partial h_j^1}{\partial w_{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] w^{21}{1j} f’(h_j^1) \frac{\partial h_j^1}{\partial w{ji}^{10}} \
& = [y(x^{(\alpha)}; w) - y_T^{(\alpha)}] \sum_{j=1}{w^{21}_{1j} S_j^1[1 - S_j^1]} x^{(\alpha)}_i
\end{align}
$$

其中已有上述结论推导出。

而：

$$
\frac{\partial h_1^2}{\partial S_j^1} = (w^{21}{1j} S_j^1 + \mathbf{bias})’ = w^{21}{1j}
$$

隐藏层的输出为，输入为，因为默认用Sigmoid为激活函数，于是有：

对于输入层，显然：

事实上对于题目的一层隐藏层，这样推导出来的误差逆传播公式基本上算是解决了问题了，若是有更多的隐藏层，无非就是根据这样的链式法则从最终输出层推导到输入层而已。

介绍完要用到的公式，那么就开始解题。

题目是构建一个单层隐藏层的MLP，使用tanh函数作为转移函数，拟合函数。

笔者偷了个懒，把MLP按照如下结构构建：

将细节完整表示：

这个时候，输入层的权重更新公式变为:

各部分更新值传递在网络中的体现：

事实上到了这里，我们基本上算是解决了这个问题，剩下的就是具体编码了，笔者的实现在Github

解题所使用的数据集

第一问是输出训练过程中误差变化：

可以看到笔者用了3000次迭代。

第二问是画出训练后3个隐藏层各自的输出：

第三问是画出训练用的输出以及训练好的网络对于样本的输出：

至于最后两问仅仅是把上面三问重复一边，对比差异，以及解释差异而已。

至此本节的解题结束。

2018-04-06

机器学习

机器学习练习笔记(二)

题目2.1 - 连结主义神经元

该练习用到的数据集Apples Oranges，数据存储两个分类，有200组数据，有两列属性以及一列分类。用简单的神经元对样本进行分类，每个样本，其中预测结果：

第一题是画散点图，因为只有x.1和x.2两个属性，并且只是一个二分类问题，笔者用R画出散点图（源码）:

可以看到，还是比较容易分类的。

然后第二题就是设置10°为间隔以及，让开始设置的两个权值，输出这些对应的分类正确率，并画图。

因为刚好只有两个属性，在二维直角坐标系中，刚好有：

将每个应用到属性集上得出，与原本的标签对比得出正确率，最后得到正确率-角度的图（源码）：

注意

笔者在第二问就尝试输出时最佳的的图像，发现直线并不是所期待一般近似划分两个类：

在开始探究原因之前，先回想清楚法向量的定义。

定义是没有问题的，那是因为刚好导致直线方程，即所得的直线刚好是法向量所在的直线，于是划分类的超平面恰好垂直于该直线，根据两直线垂直其斜率之积为可以得到最终划分超平面的超平面方程为，根据方程作出直线：

这样才有点像划分的样子，但是要注意这仅仅是时的特例，一般情况所得超平面便是划分点集的超平面。

接下来一问是根据上一问得出的最佳的，组合，得出正确率最高的（源码）：

运行得到：

接下来是根据前两问得出来的和画图（源码）：

然后就是尝试不同的组合，并画出热度图。

运行代码画图：

可以肉眼看出正确率较高时的组合在哪个部分。

笔者额外求得最高正确率时的与：

1 2	angle theta w1 w2 correctness 40 0.35 0.6427876 0.7660444 0.915

并作图：

根据方程所转化成的是没问题的，但是肉眼判断这个决策面明显达不到以上的正确率。

原因是在笔者画线是所用的方程，注意仅仅用了来生成直线，该超平面应该经过相关的点，于是便造成这样的错误，笔者并未打算在此解决这个错误，因为在以后学习LDA、SVM、PCA等问题时会解决这个问题。

题目2.2 - 多层感知机

该题目是简单地体验一下多层感知机，假设其中一层隐藏层，该层有10个感知机，通过随机生成（分别为输出权重，计算时的权重以及偏差）50次，生成50条曲线，观察现象。

第一问设置

对于：

第二问改成：

得到：

显然比第一问生成的曲线群平滑一些了，第三问当然是问观察到了什么，画一条的曲线，然后再画出平方误差最小的那条（上述两幅图用蓝色标记曲线以及误差最小的曲线）。

可以观察到误差最小时的曲线与曲线呈轴对称。

2018-04-01

工具使用

Hexo问题汇总

MathJax换行符

网上很多在Markdown中插入LaTeX公式的教程中，换行用的\\双反斜杠，在使用默认的渲染引擎时，换行不能生效，使用\newline换行是非法的。笔者猜测是引擎的渲染语义问题，一次偶然的尝试中发现用三反斜杠\\\之后可以解决问题。

但是与下一条问题一样，更换默认的渲染引擎之后可以从根本上解决这个符号语义问题，从而可以使用\\正常换行。

MathJax下划线冲突

在Markdown中渲染MathJax公式时，若下划线_随后跟着大括号{}，则这段LaTex公式会渲染失败。

解决方案，替换默认的hexo-render-marked引擎：

1 2	npm uninstall hexo-renderer-marked --save npm install hexo-renderer-kramed --save

更多详细的解决方案细节，观看源博客。

因为笔者博客主题使用的Landscape-Plus，在依据其主页指引进行安装之后，需要修改${博客根目录}/themes/landscape-plus/_config.yml中的mathjax选项开关，否则博客内的公式无法正确渲染。

插入图片

貌似Markdown原生的语法不起作用，若用其他方案则因为部署到github.io时不会自动翻译url，即使成功部署图片也会崩掉。

使用命令装上该插件：

1	$ npm install https://github.com/CodeFalling/hexo-asset-image --save # 注1

然后可以：

1	![图片的标题](${图片相对于该文件的路径或者绝对路径})

然后正常在本地，抑或部署都没有问题了。

解决方案源地址。

[注1]笔者在最近一次在新机子配置博客开发的环境时，发现直接使用npm install hexo-asset-image --save安装的插件不能正确更新图片的URL，因此改用以上的命令。

2018-03-31

数学基础

数学方法技巧整理

数据挖掘与机器学习虽然已经有了不少的开源代码可以用，但是笔者认为这两个领域的门槛并不在于代码，而在于数学。近期的学习逼得笔者开始复习本科学习高等数学、概率论以及线性代数，而用到一些较为进阶的方法则在工程优化中学习。

这篇博客主要用于整理一些数学技巧。

复合函数的积分求解技巧

设两个函数的原函数为，对于复合函数的积分。

例子：xsin(x)的不定积分

从一定程度上可以减轻求解时的头痛。

泰勒展开定义式

平面的法向量

首先回顾一下在高中所学过的平面内的直线表达式：

令向量，此时便有：

则称为直线的法向量。

CFWLoader

A man who codes for fun.

R配置Keras

环境准备

安装步骤

安装GPU支持

测试R-Keras

机器学习练习笔记(五)

题目5.1 - 交叉验证

线性代数-特征分解

特征值以及特征向量的定义

特征分解，谱分解 Eigendecomposition, Spectral Decomposition

应用1-矩阵幂的求解

奇异值分解， Singular Value Decomposition

机器学习练习笔记(四)

题目4.1 - 线性搜索

题目4.2 - 下降方法比较

拟合优度检验入门

置信度与显著性水平

注意点

Win10下gem报SSL错误的解决方案

问题现象

不推荐的解决方案

原因发现及解决方案

机器学习练习笔记(三)

题目3.1 - 误差逆向传播公式推导

题目3.2 - MLP回归

机器学习练习笔记(二)

题目2.1 - 连结主义神经元

注意

题目2.2 - 多层感知机

Hexo问题汇总

MathJax换行符

MathJax下划线冲突

插入图片

数学方法技巧整理

复合函数的积分求解技巧

例子：xsin(x)的不定积分

泰勒展开定义式

平面的法向量